题目内容
我国发射的“神舟八号”飞船与先期发射的“天宫一号”空间站实现了完美对接.已知“天宫一号”绕地球做圆轨道运动,假设沿椭圆轨道运动的“神州八号”环绕地球的运动方向与“天宫一号”相同,远地点与“天宫一号”的圆轨道相切于某点P,并在该点附近实现对接,如图所示.则下列说法正确的是:( )
| A.“天宫一号”的角速度小于地球自转的角速度 |
| B.“神舟八号”飞船的发射速度大于第一宇宙速度 |
| C.在远地点P处, “神舟八号”的加速度与“天宫一号”相等 |
| D.“神舟八号” 在椭圆轨道上运行周期比“天宫一号”在圆轨道上运行周期大 |
BC
解析试题分析:根据万有引力等于向心力: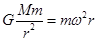 ,可求:
,可求: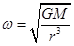 “天宫一号”的轨道半径小于同步卫星的轨道半径,所以“天宫一号”的角速度大于地球同步卫星的角速度.地球同步卫星的角速度与地球自转的角速度相同,所以“天宫一号”的角速度大于地球自转的角速度.故A错误;第一宇宙速度是发射卫星的最小速度,所以“神舟八号”飞船的发射速度大于第一宇宙速度.故B正确;根据
“天宫一号”的轨道半径小于同步卫星的轨道半径,所以“天宫一号”的角速度大于地球同步卫星的角速度.地球同步卫星的角速度与地球自转的角速度相同,所以“天宫一号”的角速度大于地球自转的角速度.故A错误;第一宇宙速度是发射卫星的最小速度,所以“神舟八号”飞船的发射速度大于第一宇宙速度.故B正确;根据 可求:
可求: 所以在远地点P处,“神舟八号”的加速度与“天宫一号”相等,故C正确;根据开普勒第三定律知,
所以在远地点P处,“神舟八号”的加速度与“天宫一号”相等,故C正确;根据开普勒第三定律知, ,“神舟八号”在椭圆轨道的半长轴小于“天宫一号”轨道半径,所以“神舟八号”在椭圆轨道上运行周期比“天宫一号”在圆轨道上运行周期小.故D错误.
,“神舟八号”在椭圆轨道的半长轴小于“天宫一号”轨道半径,所以“神舟八号”在椭圆轨道上运行周期比“天宫一号”在圆轨道上运行周期小.故D错误.
考点:本题考查天体运动。

 一线名师权威作业本系列答案
一线名师权威作业本系列答案2013年12月14日21时11分,“嫦娥三号”在月球正面的虹湾以东地区成功实现软着陆。已知月球表面的重力加速度为 g,g 为地球表面的重力加速度。月球半径为R,引力常量为G。则下列说法正确的是
g,g 为地球表面的重力加速度。月球半径为R,引力常量为G。则下列说法正确的是
A.“嫦娥三号”着陆前,在月球表面附近绕月球做匀速圆周运动的速度v = |
B.“嫦娥三号”着陆前,在月球表面附近绕月球做匀速圆周运动的周期T = |
C.月球的质量m月 =  |
D.月球的平均密度ρ =  |
2011年12月22日11时26分,我国在太原卫星发射中心用长征四号乙运载火箭,成功将“资源一号”02C卫星送入太空。至此,2011年共实施了19次航天发射任务。火箭点火起飞约13分钟后,西安卫星测控中心传来的数据表明,星箭分离,卫星成功进入离地高度约770 km的圆轨道,绕地球做匀速圆周运动。已知地球半径约为6400 km。关于“资源一号”02C卫星,下列说法正确的是
| A.它的运行速度比第一宇宙速度更大 |
| B.它的加速度比地球表面的重力加速度更小 |
| C.它的运行周期应该小于24小时 |
| D.它离地的高度比地球同步卫星更大些 |
设北斗导航系统中的地球同步卫星在距地面高度为h的同步轨道做圆周运动。已知地球的半径为R,地球表面的重力加速度为g,万有引力常量为G。下列说法正确的是( )
A.同步卫星运动的周期为 |
B.同步卫星运行的线速度为 |
C.同步轨道处的重力加速度为 |
D.地球的平均密度为 |
质量为m的人造卫星与地心距离为r时,引力势能可表示为E =-
=- ,其中G为引力常量,M为地球质量。已知地球半径为R,根据机械能守恒定律可得地球第二宇宙速度(可使卫星脱离地球引力的发射速度)为:
,其中G为引力常量,M为地球质量。已知地球半径为R,根据机械能守恒定律可得地球第二宇宙速度(可使卫星脱离地球引力的发射速度)为:
A.  | B. | C. | D.2 |
要使可视为质点的两物体间万有引力减小到原来的1/4,下列办法不可采用的是
| A.使两物体的质量各减小一半,距离不变 |
| B.使其中一个物体的质量减小到原来的1/4,距离不变 |
| C.使两物体间的距离增为原来的2倍,质量不变 |
| D.使两物体间的距离和质量都减为原来的1/4 |
发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3,轨道1、2相切于Q点,轨道2、3相切于P点,如图所示。
卫星分别在1、2、3轨道上正常运行时,以下说法正确的是________:
| A.卫星在轨道3上的速率大于在轨道1上的速率。 |
| B.卫星在轨道3上的角速度大于在轨道1上的角速度。 |
| C.卫星在轨道1上运动一周的时间小于它在轨道2上运动一周的时间。 |
| D.卫星在轨道2上经过P点时的加速度等于它在轨道3上经过P点时的加速度。 |
随着世界航空事业的发展,深太空探测已逐渐成为各国关注的热点。假设深太空中有一颗外星球,质量是地球质量的2倍,半径是地球半径的 ,则下列判断正确的是( )
,则下列判断正确的是( )
| A.该外星球的同步卫星周期一定小于地球同步卫星周期 |
| B.某物体在该外星球表面上所受重力是它在地球表面上所受重力的8倍 |
| C.该外星球上第一宇宙速度是地球上第一宇宙速度的2倍 |
| D.绕该外星球的人造卫星和以相同轨道半径绕地球的人造卫星运行速度相同 |
 倍,则太阳与地球的质量之比为:( )
倍,则太阳与地球的质量之比为:( )



