题目内容
【题目】欧洲大型强子对撞机是现在世界上最大、能量最高的粒子加速器,是一种将质子加速对撞的高能物理设备,其原理可简化如下:两束横截面积极小长度为![]() 质子束以初速度
质子束以初速度![]() 同时从左、右两侧入口射入加速电场,经过相同的一段距离后射入垂直纸面的圆形匀强磁场区域并被偏转,最后两质子束发生相碰。已知质子质量为
同时从左、右两侧入口射入加速电场,经过相同的一段距离后射入垂直纸面的圆形匀强磁场区域并被偏转,最后两质子束发生相碰。已知质子质量为![]() ,电量为
,电量为![]() ;加速极板AB、A'B'间电压均为
;加速极板AB、A'B'间电压均为![]() ,且满足
,且满足![]() 。两磁场磁感应强度相同,半径均为
。两磁场磁感应强度相同,半径均为![]() ,圆心O、O'在质子束的入射方向上,其连线与质子入射方向垂直且距离为
,圆心O、O'在质子束的入射方向上,其连线与质子入射方向垂直且距离为![]() ;整个装置处于真空中,忽略粒子间的相互作用及相对论效应。
;整个装置处于真空中,忽略粒子间的相互作用及相对论效应。
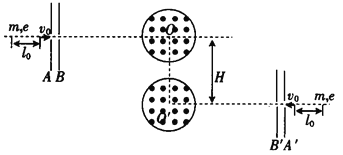
(1)试求质子束经过加速电场加速后(未进入磁场)的速度![]() 和长度
和长度![]() ;
;
(2)试求出磁场磁感应强度![]() 和粒子束可能发生碰撞的时间
和粒子束可能发生碰撞的时间![]() ;
;
(3)若某次实验时将磁场O的圆心往上移了![]() ,其余条件均不变,则质子束能否相碰?若不能,请说明理由;若能,请说明相碰的条件及可能发生碰撞的时间
,其余条件均不变,则质子束能否相碰?若不能,请说明理由;若能,请说明相碰的条件及可能发生碰撞的时间![]() 。
。
【答案】(1)v=2v0 ;L=2l0;(2)△t![]() ;(3)若t′>t.即当
;(3)若t′>t.即当![]() 时,两束粒子不会相遇;若t′<t.即当
时,两束粒子不会相遇;若t′<t.即当![]() 时,两束粒子可能相碰撞的最长时间:△t=
时,两束粒子可能相碰撞的最长时间:△t=![]()
【解析】
(1)由动能定理即可求出粒子的速度,由位移公式即可求出长度l;
(2)由半径公式即可求出磁感应强度,由位移公式即可求出时间;
(3)通过运动的轨迹与速度的方向分析能否发生碰撞.
(1)质子加速的过程中,电场力做功,得:![]()
将eU0![]() mv02代入得:v=2v0
mv02代入得:v=2v0
由于是相同的粒子,又在相同的电场中加速,所以可知,所有粒子在电场中加速的时间是相等的,在加速 之前,进入电场的时间差:![]()
出电场的时间差也是△t,所以,出电场后,该质子束的长度:L=vt=2v0t=2l0
(2)粒子在匀强磁场中做匀速圆周运动,在偏转后粒子若发生碰撞,则只有在粒子偏转90°时,才可能发生碰撞,所以碰撞的位置在OO′的连线上.
洛伦兹力提供向心力,即:![]()
所以:B![]()
由于洛伦兹力只改变磁场的方向,不改变粒子的速度,所以粒子经过磁场后的速度的大小不变,由于所有粒子的速度大小相等,所以应先后到达同一点,所以碰撞的时间:△t![]()
(3)某次实验时将磁场O的圆心往上移了![]() ,其余条件均不变,则质子束经过电场加速后的速度不变,而运动的轨迹不再对称.对于上边的粒子,不是对着圆心入射,而是从F点入射,如图:
,其余条件均不变,则质子束经过电场加速后的速度不变,而运动的轨迹不再对称.对于上边的粒子,不是对着圆心入射,而是从F点入射,如图:
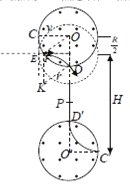
E点是原来C点的位置,连接OF、OD,作FK平行而且等于OD,再连接KD,由于OD=OF=FK,则四边形ODFK是菱形,即KD=KF,所以粒子仍然从D点射出,但方向不是沿OD的方向,K为粒子束的圆心.
由于磁场向上移了![]() ,故:
,故:![]()
得:![]() ,
,![]()
而对于下边的粒子,没有任何的改变,故两束粒子若相遇,则一定在D点相遇.
下方的粒子到达C′后先到达D点的粒子需要的时间:![]()
而上方的粒子到达E点后,最后到达D点的粒子需要的时间:![]()
若t′>t.即当![]() 时,两束粒子不会相遇;
时,两束粒子不会相遇;
若t′<t.即当![]() 时,两束粒子可能相碰撞的最长时间:△t=t﹣t′
时,两束粒子可能相碰撞的最长时间:△t=t﹣t′![]()