题目内容
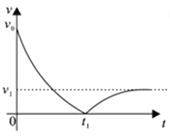
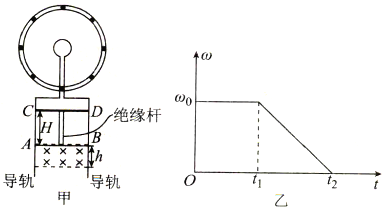
【题目】如图所示，竖直面内有一圆形小线圈，与绝缘均匀带正电圆环共面同心放置。带电圆环的带电量为Q，绕圆心做圆周运动，其角速度ω随时间t变化的关系图象如图乙所示(图中ω0、t1、t2均为已知量)。线圈通过绝缘导线连接两根竖直的、间距为l的光滑平行金属长导轨，两导轨间的矩形区域内存在垂直纸面向里的水平匀强磁场，磁场上、下边界的间距为h，磁感应强度大小恒为B．“工”字形构架由长度为H(H>h)的绝缘杆和水平金属棒AB、CD组成，金属棒与导轨紧密接触。初始时锁定“工”字形构架，使金属棒AB位于磁场内的上边沿，t1时刻解除锁定，t2时刻开始运动。已知“工”字形构架的质量为m，金属棒AB和金属棒CD的长度均为l，金属棒AB和金属棒CD离开磁场下边沿时的速度大小均为v，金属棒AB、CD和圆形线圈的电阻均为R，其余电阻不计，不考虑线圈的自感，重力加速度为g。
（1）0~t1时间内，求带电圆环的等效电流
（2）t1~t2时间内，求圆形线圈内磁通量变化率的大小
（3）求从0时刻到金属棒CD离开磁场的全过程中金属棒及线圈产生的焦耳热。
【答案】（1）
（2）
（3）
【解析】
(1)由电流的定义式可知：
(2)
时间内，由平衡条件可知：
，
则
由欧姆定律可知
，
得到：
(3)时间内，
解得：
时刻后，由功能关系可知：
得到：
从0时刻到金属棒CD离开磁场的全过程中金属棒击线圈产生的热量为：
练习册系列答案
相关题目
