题目内容
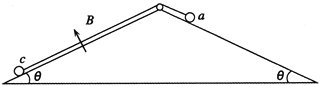
【题目】如图所示,OBAC为倾角θ=37°的固定斜面,AB部分粗糙,其余部分光滑,轻弹簧一端固定在斜面底端的挡板上,另一端与质量m=1.0 kg可视为质点的物块P接触而不拴接,物块P静止时位于A点,AB间距离L=0.10 m。第一次对P施加一平行于斜面向下的恒力F1=20 N,当P运动到B点时撤去F1,P恰好能到达斜面顶端C点。第二次对P从相同初位置开始施加一平行于斜面向下的恒力F2=100 N,当P运动到B点时撤去F2。已知运动过程中弹簧始终在弹性限度内,g=10 m/s2,sin 37°=0.6,cos 37°=0.8。在物块第二次运动过程中。

(1)求P到达C点时的速度v1;
(2)若将一半径为R=2.0 m的光滑圆弧状拱形轨道在C端与斜面相切连接(图中未画出),求P到达圆轨道最高点时对轨道的压力FN;
(3)若撤去圆形轨道,在斜面顶端C点锁定另一可视为质点的物块Q(图中未画出),当P运动到C点时,解除物块Q的锁定,P、Q发生弹性正碰,求碰后物块Q(质量未定)所能获得的最大速度。
【答案】(1)4 m/s(2)6 N(3)8.0 m/s
【解析】(1)设物块P从A经B到C过程中摩擦力做的功为Wf,重力做的功为WG,初位置弹簧的弹性势能为EP,根据动能定理有:F1L+Wf+WG+EP=0
F2L+Wf+WG+EP=![]()
解得:v1=4m/s
(2)设P到达圆形轨道最高点时的速度为v2,
由机械能守恒得:![]()
设P在最高点受轨道的支持力为FN′,由牛顿第二定律得:![]()
由牛顿第三定律得:FN=-FN′
解得:FN=6N,方向竖直向下
(3)设物块Q的质量m0,碰后P、Q的速度大小分别为vP、vQ,
由动量及能量守恒得:mv1=mvP+m0vQ
![]()
解得:![]()
当m远大于m0时,vQ最大,此时有:vQ=2v1=8.0m/s

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案