题目内容
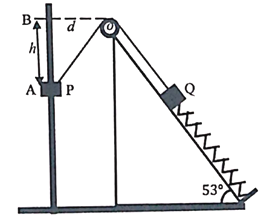
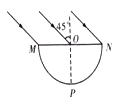
【题目】如图所示,水平面上有一半径为R的半圆柱形玻璃砖,一束平行光以45°的入射角照射到玻璃砖的上表面,已知光在此玻璃砖中的传播速度为![]() c.(光在真空中的速度为c),求:
c.(光在真空中的速度为c),求:
(1)圆柱面上光线能够从弧线MP射出的区域所对的圆心角α;
(2)能从圆柱面射出的光线中,在玻璃砖中传播的最长时间(不考虑反射光线)
【答案】(1)90°;(2)![]()
【解析】
①玻璃砖的折射率为n=![]() =
=![]() 。
。
作出光路图,如图所示。

由折射定律有:n=![]()
得:sinγ=![]() =
=![]()
解得折射角 γ=30°
如果光线EA刚好在A点发生全反射,则有:n=![]()
即有∠EAO=45°,此时∠EOA=75°
因EA与OB平行,所以∠EAO=∠AOB=45°
如果光线FC刚好在C点发生全反射,则有∠FCO=45°,此时∠FOC=15°
故知圆柱面上光线能够射出的区域所对的圆心角为:α=180°-∠EOA-∠FOC=180°-75°-15°=90°
②能从圆柱面射出的光线中,光线在玻璃砖中传播的最长距离为:s=![]()
光线在玻璃砖中传播的最长时间为:t=![]()
解得t=![]()

练习册系列答案
相关题目