��Ŀ����
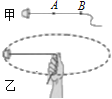
����Ŀ��һ����ϵ��Ϊk=100N/m���ᵯ���¶˹̶������Ϊ��=53���Ĺ⻬б��ˣ��϶��������Q��һ�������������O��һ�������Q���ӣ���һ�������ڹ✕��ֱ���ϵ����P���ӣ������ֵ���ֱ�˵ľ���Ϊd=0.3m����ʼʱ�����������£����P��A�㾲ֹ������������б��ƽ�У�����������СΪ50N����֪���P����Ϊm1=0.8kg�����Q����Ϊm2=5kg�����ƻ��ִ�С��Ħ��ȡ�������ٶ�g=10m/s2���ֽ����P�ɾ�ֹ�ͷţ���
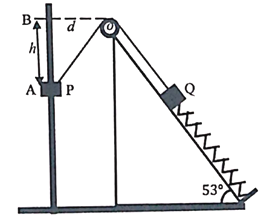
(1)���Pλ��Aʱ�����ɵ��쳤��x1�Ƕ���?
(2)���P�������뻬��O�ȸߵ�B��ʱ�����Q���ٶ��Ƕ��?
(3)��A��B���h=0.4m�������P������B��Ĺ����У��������������P���Ĺ���
���𰸡���1��0.1 m��2��0��3��8 J
��������
��1������Pλ��A�㣬���赯���쳤��Ϊx1����
T=m2gsin��+kx1
��ã�x1=0.1 m
��2�����P�������뻬��O�ȸߵ�B��ʱ��OB��ֱ��ֱ�ˣ����Q�ٶ�Ϊ0��
��3������������A��B���h=0.4 m����ʱOB��ֱ��ֱ�ˣ���OB=d=0.3 m����ʱ���Q�½�����Ϊ����x=OP-OB=0.2 m
������ѹ�� ��x2=��x-x1=0.1m���������ܲ��䡣
������P��Q�����ɣ���A��B���������غ��У�
![]()
����ɵã� ![]()
�����P�� ![]()
�������ݵ� WT=8 J

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�