题目内容
9.电子以3.2×106m/s速率垂直射入B=0.91×10-4T的匀强磁场中,求电子做圆周运动的轨道半径R和周期T(已知电子的电量e=-1.6×10-19C,质量m=9.1×10-31Kg,结果保留两位有效数字).分析 电子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律求出电子的轨道半径,然后求出电子的周期.
解答 解:电子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:
evB=m$\frac{{v}^{2}}{r}$,则有r=$\frac{mv}{eB}$,
代入数据解得:r=$\frac{9.1×1{0}^{-31}×3.2×1{0}^{6}}{1.6×1{0}^{-19}×0.91×1{0}^{-4}}$=0.2m;
电子做圆周运动的周期为:
T=$\frac{2πr}{v}$=$\frac{2πm}{eB}$,
代入数据解得:T=$\frac{2×π×9.1×1{0}^{-31}}{1.6×1{0}^{-19}×0.91×1{0}^{-4}}$=3.9×10-7s;
答:电子做圆周运动的轨道半径为0.2m,周期为3.9×10-7s.
点评 本题考查了求电子的轨道半径与周期,应用牛顿第二定律与周期公式即可正确解题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
20. 如图所示,在光滑的水平面上,一质量为m=0.1kg,半径为r=0.5m,电阻为R=0.5Ω的均匀金属圆环,以v0=5m/s的初速度向?一磁感应强度为B=0.1T的有界匀强磁场滑去(磁场宽度d>2r),圆环的一半进入磁场历时2秒,圆环上产生的焦耳热为0.5J,则2s末圆环中感应电流的瞬时功率为( )
如图所示,在光滑的水平面上,一质量为m=0.1kg,半径为r=0.5m,电阻为R=0.5Ω的均匀金属圆环,以v0=5m/s的初速度向?一磁感应强度为B=0.1T的有界匀强磁场滑去(磁场宽度d>2r),圆环的一半进入磁场历时2秒,圆环上产生的焦耳热为0.5J,则2s末圆环中感应电流的瞬时功率为( )
 如图所示,在光滑的水平面上,一质量为m=0.1kg,半径为r=0.5m,电阻为R=0.5Ω的均匀金属圆环,以v0=5m/s的初速度向?一磁感应强度为B=0.1T的有界匀强磁场滑去(磁场宽度d>2r),圆环的一半进入磁场历时2秒,圆环上产生的焦耳热为0.5J,则2s末圆环中感应电流的瞬时功率为( )
如图所示,在光滑的水平面上,一质量为m=0.1kg,半径为r=0.5m,电阻为R=0.5Ω的均匀金属圆环,以v0=5m/s的初速度向?一磁感应强度为B=0.1T的有界匀强磁场滑去(磁场宽度d>2r),圆环的一半进入磁场历时2秒,圆环上产生的焦耳热为0.5J,则2s末圆环中感应电流的瞬时功率为( )| A. | 0.15W | B. | 0.2W | C. | 0.3W | D. | 0.6W |
4. A,B两球用细线悬挂于天花板上且静止不动,两球质量之比mA:mB=5:3.两球间连接一个轻弹簧(如图所示),如果突然剪断细线,则在剪断细线瞬间A球、B球的加速度分为(已知重力加速度为g)( )
A,B两球用细线悬挂于天花板上且静止不动,两球质量之比mA:mB=5:3.两球间连接一个轻弹簧(如图所示),如果突然剪断细线,则在剪断细线瞬间A球、B球的加速度分为(已知重力加速度为g)( )
 A,B两球用细线悬挂于天花板上且静止不动,两球质量之比mA:mB=5:3.两球间连接一个轻弹簧(如图所示),如果突然剪断细线,则在剪断细线瞬间A球、B球的加速度分为(已知重力加速度为g)( )
A,B两球用细线悬挂于天花板上且静止不动,两球质量之比mA:mB=5:3.两球间连接一个轻弹簧(如图所示),如果突然剪断细线,则在剪断细线瞬间A球、B球的加速度分为(已知重力加速度为g)( )| A. | g,g | B. | 1.6g,0 | C. | 0.6g,0 | D. | 0,$\frac{8}{3}$g |
2.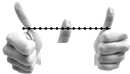 为了研究合力和分力的大小,某两个同学做了如下实验,甲同学用把栓校牌的细绳用两手拉直,乙同学用一个手指轻轻一推,如图所示,对将可能发生的情况,以下说法正确的是( )
为了研究合力和分力的大小,某两个同学做了如下实验,甲同学用把栓校牌的细绳用两手拉直,乙同学用一个手指轻轻一推,如图所示,对将可能发生的情况,以下说法正确的是( )
 为了研究合力和分力的大小,某两个同学做了如下实验,甲同学用把栓校牌的细绳用两手拉直,乙同学用一个手指轻轻一推,如图所示,对将可能发生的情况,以下说法正确的是( )
为了研究合力和分力的大小,某两个同学做了如下实验,甲同学用把栓校牌的细绳用两手拉直,乙同学用一个手指轻轻一推,如图所示,对将可能发生的情况,以下说法正确的是( )| A. | 因为甲同学用两只手用力拉直细绳,所以乙同学需很大的力才能推动细绳 | |
| B. | 根据力的合成与分解原理可知,乙同学只要轻轻用力沿着同绳垂直的方向推细绳,细绳就会发生弯曲 | |
| C. | 根据实践经验可知,乙同学不需用太大的力,就能使细绳发生弯曲 | |
| D. | 以上说法都不对 |
20. 如图所示水平粗糙地面上放置一斜面,CD段光滑,DE段粗糙,A、B两物体叠放在一起从C点由静止下滑,下滑过程中斜面保持静止,A、B始终保持相对静止,则( )
如图所示水平粗糙地面上放置一斜面,CD段光滑,DE段粗糙,A、B两物体叠放在一起从C点由静止下滑,下滑过程中斜面保持静止,A、B始终保持相对静止,则( )
 如图所示水平粗糙地面上放置一斜面,CD段光滑,DE段粗糙,A、B两物体叠放在一起从C点由静止下滑,下滑过程中斜面保持静止,A、B始终保持相对静止,则( )
如图所示水平粗糙地面上放置一斜面,CD段光滑,DE段粗糙,A、B两物体叠放在一起从C点由静止下滑,下滑过程中斜面保持静止,A、B始终保持相对静止,则( )| A. | 在CD段时,A只受两个力作用 | |
| B. | 在DE段时,A受摩擦力一定沿斜面向上 | |
| C. | 整个下滑过程中,A、B均处于失重状态 | |
| D. | 整个下滑过程中,斜面一直受地面的摩擦力作用 |
 如图甲所示,长、宽分别为L1=0.1m、L2=0.2m的矩形金属线框位于竖直平面内,其匝数为100匝,总电阻为1Ω,可绕其竖直中心轴O1O2转动.线框的两个末端分别与两个彼此绝缘的铜环C、D(集流环)焊接在一起,并通过电刷和定值电阻R=9Ω相连.线框所在空间有水平向右均匀分布的磁场,磁感应强度B的大小随时间t的变化关系如图乙所示,其中B0=5×10-3 T、B1=1×10-2 T和t1=2×10-3S.在0~t1的时间内,线框保持静止,且线框平面和磁场垂直;t1时刻后线框在外力的驱动下开始绕其竖直中心轴以角速度ω=200rad/s匀速转动.求:
如图甲所示,长、宽分别为L1=0.1m、L2=0.2m的矩形金属线框位于竖直平面内,其匝数为100匝,总电阻为1Ω,可绕其竖直中心轴O1O2转动.线框的两个末端分别与两个彼此绝缘的铜环C、D(集流环)焊接在一起,并通过电刷和定值电阻R=9Ω相连.线框所在空间有水平向右均匀分布的磁场,磁感应强度B的大小随时间t的变化关系如图乙所示,其中B0=5×10-3 T、B1=1×10-2 T和t1=2×10-3S.在0~t1的时间内,线框保持静止,且线框平面和磁场垂直;t1时刻后线框在外力的驱动下开始绕其竖直中心轴以角速度ω=200rad/s匀速转动.求: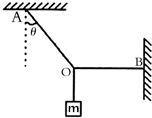 如图所示,细线的一端固定于A点,细线上挂一质量为m的物体,另一端B固定在墙上,当AO与竖直方向成θ角,OB沿水平方向时,则:AO及BO对O点的拉力分别是多大?
如图所示,细线的一端固定于A点,细线上挂一质量为m的物体,另一端B固定在墙上,当AO与竖直方向成θ角,OB沿水平方向时,则:AO及BO对O点的拉力分别是多大? 如图所示,细绳AB和BC共同吊起一个重10N的物体,AC和BC垂直,绳AC与墙面夹角为60°,求出轻绳AC和BC的张力大小.
如图所示,细绳AB和BC共同吊起一个重10N的物体,AC和BC垂直,绳AC与墙面夹角为60°,求出轻绳AC和BC的张力大小.