题目内容
17.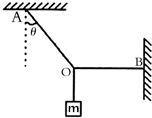 如图所示,细线的一端固定于A点,细线上挂一质量为m的物体,另一端B固定在墙上,当AO与竖直方向成θ角,OB沿水平方向时,则:AO及BO对O点的拉力分别是多大?
如图所示,细线的一端固定于A点,细线上挂一质量为m的物体,另一端B固定在墙上,当AO与竖直方向成θ角,OB沿水平方向时,则:AO及BO对O点的拉力分别是多大?
分析 对O点受力分析,受重力和两个拉力,根据平衡条件并结合分解法列式求解即可.
解答  解:根据O点受力由正交分解有:
解:根据O点受力由正交分解有:
FOAcosθ=G…①
FOAsinθ=FOB …②
联立①②,解得:
FOA=$\frac{mg}{cosθ}$,
FOB=mgtanθ,
根据牛顿第三定律可知,AO及BO对O点的拉力分别是$\frac{mg}{cosθ}$和mgtanθ.
答:AO及BO对O点的拉力分别是$\frac{mg}{cosθ}$和mgtanθ.
点评 本题关键对O点受力分析后根据平衡条件列式求解,可以结合合成法、分解法、正交分解法求解,基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7. 如图所示,一竖直平面内的光滑圆形轨道半径为R,小球以速度v0经过最低点B沿轨道上滑,并恰能通过轨道最高点A.以下说法正确的是( )
如图所示,一竖直平面内的光滑圆形轨道半径为R,小球以速度v0经过最低点B沿轨道上滑,并恰能通过轨道最高点A.以下说法正确的是( )
 如图所示,一竖直平面内的光滑圆形轨道半径为R,小球以速度v0经过最低点B沿轨道上滑,并恰能通过轨道最高点A.以下说法正确的是( )
如图所示,一竖直平面内的光滑圆形轨道半径为R,小球以速度v0经过最低点B沿轨道上滑,并恰能通过轨道最高点A.以下说法正确的是( )| A. | v0应等于2$\sqrt{gR}$ | |
| B. | 运动过程中,小球受到的合外力提供向心力 | |
| C. | 小球在B点时加速度最大,在A点时加速度最小 | |
| D. | 小球从B点到A点,其速度的增量为(1+$\sqrt{5}$)$\sqrt{gR}$ |
8.一竖直悬挂的轻质弹簧下端不挂物体时长度是10cm,在其下端悬挂一质量为0.1kg的物体,当物体静止后,弹簧的长度为11cm,取g=10m/s2.该弹簧的劲度系数为( )
| A. | 1N/m | B. | 10N/m | C. | 100N/m | D. | 1000N/m |
5. 木块原来放在水平长木板上,两接触面的动摩擦因数为$\frac{1}{\sqrt{3}}$,把长木板的一端向上抬起,当长木板与水平面的夹角为多少时,木块将要滑下来?(设最大静摩擦力与滑动摩擦力相等)
木块原来放在水平长木板上,两接触面的动摩擦因数为$\frac{1}{\sqrt{3}}$,把长木板的一端向上抬起,当长木板与水平面的夹角为多少时,木块将要滑下来?(设最大静摩擦力与滑动摩擦力相等)
 木块原来放在水平长木板上,两接触面的动摩擦因数为$\frac{1}{\sqrt{3}}$,把长木板的一端向上抬起,当长木板与水平面的夹角为多少时,木块将要滑下来?(设最大静摩擦力与滑动摩擦力相等)
木块原来放在水平长木板上,两接触面的动摩擦因数为$\frac{1}{\sqrt{3}}$,把长木板的一端向上抬起,当长木板与水平面的夹角为多少时,木块将要滑下来?(设最大静摩擦力与滑动摩擦力相等)
2.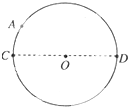 如图所示,一半径为R的圆内有垂直纸面的匀强磁场,磁感应强度为B,CD是该圆一直径.一质量m、电荷量q的带电粒子(不计重力),自A点沿指向O点的方向垂直射入磁场中,恰好从D点飞出磁场,A点到CD的距离为$\frac{R}{2}$,根据以上内容( )
如图所示,一半径为R的圆内有垂直纸面的匀强磁场,磁感应强度为B,CD是该圆一直径.一质量m、电荷量q的带电粒子(不计重力),自A点沿指向O点的方向垂直射入磁场中,恰好从D点飞出磁场,A点到CD的距离为$\frac{R}{2}$,根据以上内容( )
 如图所示,一半径为R的圆内有垂直纸面的匀强磁场,磁感应强度为B,CD是该圆一直径.一质量m、电荷量q的带电粒子(不计重力),自A点沿指向O点的方向垂直射入磁场中,恰好从D点飞出磁场,A点到CD的距离为$\frac{R}{2}$,根据以上内容( )
如图所示,一半径为R的圆内有垂直纸面的匀强磁场,磁感应强度为B,CD是该圆一直径.一质量m、电荷量q的带电粒子(不计重力),自A点沿指向O点的方向垂直射入磁场中,恰好从D点飞出磁场,A点到CD的距离为$\frac{R}{2}$,根据以上内容( )| A. | 可判别圆内的匀强磁场的方向垂直纸面向里 | |
| B. | 不可求出粒子在磁场中做圆周运动的轨道半径 | |
| C. | 可求得粒子在磁场中的运动时间 | |
| D. | 不可求得粒子进入磁场时的速度 |
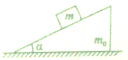 质量为m的物体放在斜面上,恰好沿倾角为α的斜面匀速下滑,而质量为m0的斜面始终与水平地面保持静止,如图所示,求物体下滑过程中,地面对斜面体的支持力以及摩擦力.(用隔离法与整体法两种方法求解)
质量为m的物体放在斜面上,恰好沿倾角为α的斜面匀速下滑,而质量为m0的斜面始终与水平地面保持静止,如图所示,求物体下滑过程中,地面对斜面体的支持力以及摩擦力.(用隔离法与整体法两种方法求解)