题目内容
12.A、B两球在水平光滑轨道上同向运动,已知它们的动量分别是PA=5㎏•m/s,PB=7㎏•m/s.A从后面追上B并发生碰撞,碰后B球的动量变为10㎏•m/s.则两球质量mA、mB的关系中,下列哪个是可能的( )| A. | mA=mB | B. | mA=$\frac{{m}_{B}}{2}$ | C. | mA=$\frac{{m}_{B}}{4}$ | D. | mA=$\frac{{m}_{B}}{8}$ |
分析 两球碰撞过程遵守动量守恒定律,由动量守恒求出碰撞后甲的动量.根据甲球速度大于乙球速度,以及碰撞过程中总动能不增加,列出不等式,求出甲与乙质量比值的范围进行选择.
解答 解:A从后面追上B并发生碰撞,说明A的速度大于B的速度,
则有:$\frac{{P}_{A}}{{m}_{A}}$>$\frac{{P}_{B}}{{m}_{B}}$,解得:$\frac{{m}_{A}}{{m}_{B}}$<$\frac{{P}_{A}}{{P}_{B}}$=$\frac{5}{7}$,
碰撞过程系统动量守恒,以A的初速度方向为正方向,
由动量守恒定律得:PA+PB=PA′+PB′,解得:PA′=2kg•m/s.
碰撞过程总动能不增加:$\frac{{P}_{A}^{2}}{2{m}_{A}}$+$\frac{{P}_{B}^{2}}{2{m}_{B}}$≥$\frac{P{′}_{A}^{2}}{2{m}_{A}}$+$\frac{P{′}_{B}^{2}}{2{m}_{B}}$,整理得:$\frac{{m}_{A}}{{m}_{B}}$<$\frac{7}{17}$,
碰撞后两球同向运动,甲的速度不大于乙的速度,则$\frac{{P}_{A}′}{{m}_{A}}$≤$\frac{{P}_{B}′}{{m}_{B}}$,整理得:$\frac{{m}_{A}}{{m}_{B}}$≥$\frac{1}{5}$,
综上所述可知:$\frac{1}{5}$≤$\frac{{m}_{A}}{{m}_{B}}$≤$\frac{7}{17}$;
故选:C.
点评 本题考查对碰撞规律的理解和应用能力.碰撞有三个基本规律:一、动量守恒;二、系统总动能不增加;三、碰撞后如同向运动,后面的物体的速度不大于前面物体的速度,即要符合实际运动情况.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案| A. | 原来有某种放射性元素的原子核500个,经过1个半衰期T后,一定仅剩250个该发射性原子核未发生衰变 | |
| B. | 光电效应实验中,光电子的最大初动能与入射光的频率有关 | |
| C. | 天然发射现象中发射出的α、β、γ三种射线,γ射线的穿透能力最强 | |
| D. | 结合能越大,表示原子核结合得越牢固 | |
| E. | 根据波尔理论,氢原子的核外电子由高能级跃迁到低能级时,要释放出一定频率的光子,同时电子的动能增加,势能减少 |
| A. | 每节课40分钟 | B. | 运动员跑完100m用了10s | ||
| C. | 物理考试10:00结束 | D. | 物体在前5秒内的位移为10m |
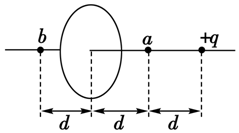 如图所示,有一带电量为+q的点电荷与均匀带电的圆形薄板相距为2d,圆形薄板带电量为-Q,点电荷到带电薄板的垂线通过板的圆心,若图中b点处的电场强度为零,则图中a点处的电场强度大小是( )
如图所示,有一带电量为+q的点电荷与均匀带电的圆形薄板相距为2d,圆形薄板带电量为-Q,点电荷到带电薄板的垂线通过板的圆心,若图中b点处的电场强度为零,则图中a点处的电场强度大小是( )| A. | $\frac{10kq}{9{d}^{2}}$ | B. | $\frac{8kq}{9{d}^{2}}$ | C. | $\frac{k(Q+q)}{{d}^{2}}$ | D. | $\frac{kq}{{d}^{2}}$ |
| A. | 做匀速直线运动 | B. | 做匀速圆周运动 | ||
| C. | 做匀加速直线运动 | D. | 静止不动 |
 某同学站在观光电梯地板上,用加速度传感器记录了电梯由静止开始运动的加速度随时间变化情况,以竖直向上为正方向.根据a-t图象提供的信息,g取10m/s2,求:
某同学站在观光电梯地板上,用加速度传感器记录了电梯由静止开始运动的加速度随时间变化情况,以竖直向上为正方向.根据a-t图象提供的信息,g取10m/s2,求: 轻质杠杆长为L=1.0m,两端各焊有一个质量为m=1.0kg的小球A、B,在距A段$\frac{L}{4}$处安装一个水平转轴O,使杠杆竖直挂在O上处于静止状态,如图所示,今用榔头猛然水平敲击A,使球A获得一定的水平速度vA,求此时:
轻质杠杆长为L=1.0m,两端各焊有一个质量为m=1.0kg的小球A、B,在距A段$\frac{L}{4}$处安装一个水平转轴O,使杠杆竖直挂在O上处于静止状态,如图所示,今用榔头猛然水平敲击A,使球A获得一定的水平速度vA,求此时: 在如图所示的电路中,小灯泡L标有“3V 1.8W”,定值电阻R1=3.5Ω、R2=7.5Ω.电源的内阻r=0.5Ω,电流表为理想电流表.滑动变阻器的滑片P滑到最左端B位置时,电流的表示数为1.5A,当滑片P滑到最右端A时、小灯泡L恰好正常发光,求:
在如图所示的电路中,小灯泡L标有“3V 1.8W”,定值电阻R1=3.5Ω、R2=7.5Ω.电源的内阻r=0.5Ω,电流表为理想电流表.滑动变阻器的滑片P滑到最左端B位置时,电流的表示数为1.5A,当滑片P滑到最右端A时、小灯泡L恰好正常发光,求: