题目内容
17. 某同学站在观光电梯地板上,用加速度传感器记录了电梯由静止开始运动的加速度随时间变化情况,以竖直向上为正方向.根据a-t图象提供的信息,g取10m/s2,求:
某同学站在观光电梯地板上,用加速度传感器记录了电梯由静止开始运动的加速度随时间变化情况,以竖直向上为正方向.根据a-t图象提供的信息,g取10m/s2,求:(1)前35s内最大的加速度是多少?
(2)设该同学质量为50kg,请画出他对电梯地板压力随时间变化的图象;
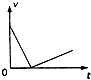
(3)如图是电梯运动的a-x图象,横轴为电梯上升的位移,求x=15m时电梯的速度.
分析 (1)由图直接前35s内最大的加速度.
(2)根据牛顿第二定律求出各段时间内电梯对人的支持力,再由牛顿第三定律人对电梯的压力,即可画出图象.
(3)根据动能定理求x=15m时电梯的速度.
解答  解:(1)由图甲知,前35s内电梯的最大加速度0.4m/s2.
解:(1)由图甲知,前35s内电梯的最大加速度0.4m/s2.
(2)根据牛顿第二定律得:
0-5s内,有:N1-mg=ma1;得 N1=m(g+a1)=50×(10+0.2)=510N,由牛顿第三定律得知,人对电梯的压力大小为510N,方向竖直向下,为负值.
5s-15s内,有:N2-mg=ma2;得 N2=mg+ma2,可知,加速度均匀减小,支持力减小,则人对电梯的压力均匀减小,方向竖直向下,为负值.
15s-25s内,N3-mg=0,N3=500N,由牛顿第三定律得知,人对电梯的压力大小为500N,方向竖直向下,为负值.
t=25s时,有mg-N4=ma4;得N4=m(g-a4)=50×(10-0.4)N=480N,由牛顿第三定律得知,人对电梯的压力大小为480N,方向竖直向下,为负值.
25-35s内,有:mg-N5=ma5;N5=mg-ma5,可知随着加速度的减小,支持力均匀减小,则人对电梯的压力均匀减小,方向竖直向下,为负值.
t=35s时,N6-mg=0,N6=500N,由牛顿第三定律得知,人对电梯的压力大小为500N,方向竖直向下,为负值.
画出他对电梯地板压力随时间变化的图象如图.
(3)根据动能定理得:W合=$\frac{1}{2}m{v}^{2}$
又W合=F合x=max,可知图象与坐标轴所围的面积再乘以m表示合力做功,由图象可得:
W合=m$\frac{5+15}{2}×$0.2J=100J
则得:v=2m/s
答:
(1)前35s内电梯的最大加速度0.4m/s2.
(2)如图所示.
(3)x=15m时电梯的速度是2m/s.
点评 解决本题的关键要正确运用牛顿运动定律研究支持力和压力,知道a-x图象的面积乘以质量等于合力做功.

 如图所示电路中,A、B两灯均正常发光,R为一滑动变阻器,P为滑动片,若将滑动片向上滑动,则( )
如图所示电路中,A、B两灯均正常发光,R为一滑动变阻器,P为滑动片,若将滑动片向上滑动,则( )| A. | 电源总功率变大 | B. | B灯变暗 | ||
| C. | R1上消耗功率变小 | D. | 流过R的电流变大 |
| A. | mA=mB | B. | mA=$\frac{{m}_{B}}{2}$ | C. | mA=$\frac{{m}_{B}}{4}$ | D. | mA=$\frac{{m}_{B}}{8}$ |
| A. | v0=$\sqrt{gR}$ | |
| B. | v0=$\sqrt{gRtanθ}$ | |
| C. | 若v>v0,则路面对车轮产生的横向摩擦力大小为m$\frac{{v}^{2}}{R}$cosθ-mgsinθ | |
| D. | 若v>v0,则路面对车轮产生的横向摩擦力大小为mgsinθ-m$\frac{{v}^{2}}{R}$cosθ |
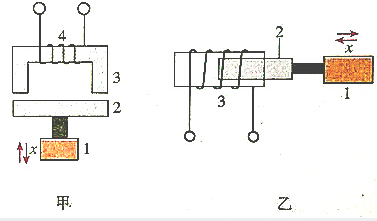
 如图所示,竖直放置在水平地面上的轻弹簧,下端固定在地面上,将一个金属球放置在弹簧顶端(球与弹簧不粘连),并用力向下压球.稳定后用细线把弹簧拴牢.烧断细线,球将被弹起,脱离弹簧后能继续向上运动,则该球从细线被烧断到刚脱离弹簧的运动过程中( )
如图所示,竖直放置在水平地面上的轻弹簧,下端固定在地面上,将一个金属球放置在弹簧顶端(球与弹簧不粘连),并用力向下压球.稳定后用细线把弹簧拴牢.烧断细线,球将被弹起,脱离弹簧后能继续向上运动,则该球从细线被烧断到刚脱离弹簧的运动过程中( )| A. | 球的机械能守恒 | |
| B. | 球的动能先增大后减小,机械能一直增加 | |
| C. | 球脱离弹簧时弹簧的长度小于原长 | |
| D. | 球在刚脱离弹簧时动能最大 |
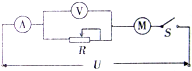 如图所示的电路中,电源电压U恒为36V.闭合电键S,当调节滑动变阻器R并控制电动机停止转动时,理想电流表和电压表的示数分别为0.5A和34V,重新调节R并使电动机恢复正常运转,此时理想电流表和电压表的示数分别为2.0A和12V.求:
如图所示的电路中,电源电压U恒为36V.闭合电键S,当调节滑动变阻器R并控制电动机停止转动时,理想电流表和电压表的示数分别为0.5A和34V,重新调节R并使电动机恢复正常运转,此时理想电流表和电压表的示数分别为2.0A和12V.求: