题目内容
2.在真空中两个等量异号点电荷,电荷量的数值均为1×10-6C.相距10cm,静电力常量k=9.0×109N•m2/C2.则它们之间的相互作用力为0.9N.在两者连线的中点处,电场强度大小为7.2ⅹ106N/C.分析 根据库仑定律求解与两电荷间的作用力.根据点电荷场强公式分别求出两点电荷在中点处产生的场强,再进行合成,求出合场强.
解答 解:已知真空中两点电荷的电量均为q=1×10-6C,距离r=0.1m,根据库仑定律得
电荷间的作用力F=k$\frac{{q}^{2}}{{r}^{2}}$=9×109×$\frac{(1×1{0}^{-6})^{2}}{0.{1}^{2}}$N=0.9N;
两点电荷在中点处产生的场强大小为E=k$\frac{q}{(\frac{r}{2})^{2}}$=$\frac{9×1{0}^{9}×1×1{0}^{-6}}{0.0{5}^{2}}$=3.6×106N/C,方向相同,
则在两者连线的中点处,电场强度大小为E合=2E=7.2×106N/C;
故答案为:0.9;7.2ⅹ106.
点评 本题两电荷连线上电场强度是两电荷产生的电场强度的叠加,根据平行四边形定则进行合成.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.如图所示,小球A与物块B的质量分别为m和M,开始B静止,而A则由静止开始从B内半径为R的半圆弧曲面轨道的边缘释放,若不计一切摩擦,则B所能获得的最大速度为( )
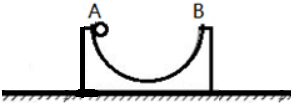

| A. | M$\sqrt{\frac{2gR}{M(M-m)}}$ | B. | m$\sqrt{\frac{2gR}{M(M-m)}}$ | C. | M$\sqrt{\frac{2gR}{M(M+m)}}$ | D. | m$\sqrt{\frac{2gR}{M(M+m)}}$ |
13.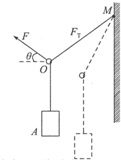 如图所示,一轻绳的一端系在竖直墙上M点,轻绳穿过一轻质光滑圆环O,另一端系一质量为m的物体A.现用力F拉住轻环上一点,使物体A从图中虚线位置缓慢上升到实线位置.则在此过程中,绳中张力FT、力F和力F与水平方向夹角θ的变化情况正确的是( )
如图所示,一轻绳的一端系在竖直墙上M点,轻绳穿过一轻质光滑圆环O,另一端系一质量为m的物体A.现用力F拉住轻环上一点,使物体A从图中虚线位置缓慢上升到实线位置.则在此过程中,绳中张力FT、力F和力F与水平方向夹角θ的变化情况正确的是( )
 如图所示,一轻绳的一端系在竖直墙上M点,轻绳穿过一轻质光滑圆环O,另一端系一质量为m的物体A.现用力F拉住轻环上一点,使物体A从图中虚线位置缓慢上升到实线位置.则在此过程中,绳中张力FT、力F和力F与水平方向夹角θ的变化情况正确的是( )
如图所示,一轻绳的一端系在竖直墙上M点,轻绳穿过一轻质光滑圆环O,另一端系一质量为m的物体A.现用力F拉住轻环上一点,使物体A从图中虚线位置缓慢上升到实线位置.则在此过程中,绳中张力FT、力F和力F与水平方向夹角θ的变化情况正确的是( )| A. | FT保持不变,F保持不变,夹角θ逐渐减小 | |
| B. | FT保持不变,F逐渐增大,夹角θ逐渐增大 | |
| C. | FT逐渐增大,F逐渐减小,夹角θ逐渐减小 | |
| D. | FT逐渐减小,F保持不变,夹角θ逐渐增大 |
10.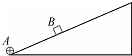 如图所示,光滑绝缘的斜面底端固定着一个带正电的小物体A,将另一个带电小物体B在斜面的某位置由静止释放,它将沿斜面向上运动.设斜面足够长,则在_B向上运动过程中( )
如图所示,光滑绝缘的斜面底端固定着一个带正电的小物体A,将另一个带电小物体B在斜面的某位置由静止释放,它将沿斜面向上运动.设斜面足够长,则在_B向上运动过程中( )
 如图所示,光滑绝缘的斜面底端固定着一个带正电的小物体A,将另一个带电小物体B在斜面的某位置由静止释放,它将沿斜面向上运动.设斜面足够长,则在_B向上运动过程中( )
如图所示,光滑绝缘的斜面底端固定着一个带正电的小物体A,将另一个带电小物体B在斜面的某位置由静止释放,它将沿斜面向上运动.设斜面足够长,则在_B向上运动过程中( )| A. | 物体B的动能一直增大 | |
| B. | 物体B的机械能一直增大 | |
| C. | 物体A、B之间的电势能一直减小 | |
| D. | 物体A、B的机械能和电势能之和先增大后减小 |
17.一个电流表G,它的内阻是100Ω,满偏电流是2mA,若要把它改装成量程为1A的电流表.则电流表G应( )
| A. | 并联0.2Ω的电阻 | B. | 并联0.02Ω的电阻 | C. | 并联50Ω的电阻 | D. | 并联4900Ω的电阻 |
7. 如图所示电路中,A、B两灯均正常发光,R为一滑动变阻器,P为滑动片,若将滑动片向上滑动,则( )
如图所示电路中,A、B两灯均正常发光,R为一滑动变阻器,P为滑动片,若将滑动片向上滑动,则( )
 如图所示电路中,A、B两灯均正常发光,R为一滑动变阻器,P为滑动片,若将滑动片向上滑动,则( )
如图所示电路中,A、B两灯均正常发光,R为一滑动变阻器,P为滑动片,若将滑动片向上滑动,则( )| A. | 电源总功率变大 | B. | B灯变暗 | ||
| C. | R1上消耗功率变小 | D. | 流过R的电流变大 |
14. 如图,R1和R2是材料相同、厚度相同、表面都为正方形的导体,R1的表面边长是R2的表面边长的2倍,则R1和R2的大小关系是( )
如图,R1和R2是材料相同、厚度相同、表面都为正方形的导体,R1的表面边长是R2的表面边长的2倍,则R1和R2的大小关系是( )
 如图,R1和R2是材料相同、厚度相同、表面都为正方形的导体,R1的表面边长是R2的表面边长的2倍,则R1和R2的大小关系是( )
如图,R1和R2是材料相同、厚度相同、表面都为正方形的导体,R1的表面边长是R2的表面边长的2倍,则R1和R2的大小关系是( )| A. | R1>R2 | B. | R1=R2 | C. | R1<R2 | D. | 无法判断 |
11.某点电荷和金属环间的电场线分布如图所示,以下说法正确的是( )


| A. | a点的电势高于b点的电势 | |
| B. | c点的电场强度与d点的电场强度大小关系无法判断 | |
| C. | 若将一正试探电荷由a点移到b点,电场力做负功 | |
| D. | 若将一正试探电荷从d点由静止释放,电荷将沿着电场线由d到c |
12.A、B两球在水平光滑轨道上同向运动,已知它们的动量分别是PA=5㎏•m/s,PB=7㎏•m/s.A从后面追上B并发生碰撞,碰后B球的动量变为10㎏•m/s.则两球质量mA、mB的关系中,下列哪个是可能的( )
| A. | mA=mB | B. | mA=$\frac{{m}_{B}}{2}$ | C. | mA=$\frac{{m}_{B}}{4}$ | D. | mA=$\frac{{m}_{B}}{8}$ |