题目内容
4. 轻质杠杆长为L=1.0m,两端各焊有一个质量为m=1.0kg的小球A、B,在距A段$\frac{L}{4}$处安装一个水平转轴O,使杠杆竖直挂在O上处于静止状态,如图所示,今用榔头猛然水平敲击A,使球A获得一定的水平速度vA,求此时:
轻质杠杆长为L=1.0m,两端各焊有一个质量为m=1.0kg的小球A、B,在距A段$\frac{L}{4}$处安装一个水平转轴O,使杠杆竖直挂在O上处于静止状态,如图所示,今用榔头猛然水平敲击A,使球A获得一定的水平速度vA,求此时:(1)vA=1.0m/s时,轴O所受的力;
(2)vA=2.0m/s时,轴O所受的力(g取10m/s2).
分析 分别对A、B两球分析,根据牛顿第二定律求出杆子对小球的作用力,从而得出球对杆子的作用力,得出轴O所受的作用力.
解答 解:(1)对A球,设杆对A球的作用力向下.根据牛顿第二定律得:
F1+mg=m$\frac{{v}_{A}^{2}}{\frac{L}{4}}$
得:F1=m($\frac{{v}_{A}^{2}}{\frac{L}{4}}$-g)=1×($\frac{{1}^{2}}{\frac{1}{4}}$-10)N=-6N,说明杆对A球的作用力方向竖直向上,大小为6N.
根据牛顿第三定律可得A球对杆的作用力大小为6N,方向竖直向下.
由v=ωr,ω相等,可知B球的速度为:vB=3vA=3m/s
对B球,根据牛顿第二定律得:F2-mg=m$\frac{{v}_{B}^{2}}{\frac{3}{4}L}$,
解得:F2=22N.
由牛顿第三定律得,B球对杆的作用力大小为22N,方向竖直向下.
因此轴O所受的力大小为 FO=|F1|+F2=28N,方向竖直向下.
(2)同理,当vA=2.0m/s时,对A球,设杆对A球的作用力向下.根据牛顿第二定律得:
F1+mg=m$\frac{{v}_{A}^{2}}{\frac{L}{4}}$
得:F1=m($\frac{{v}_{A}^{2}}{\frac{L}{4}}$-g)=1×($\frac{{2}^{2}}{\frac{1}{4}}$-10)N=6N,说明杆对A球的作用力方向竖直向下,大小为6N.
根据牛顿第三定律可得A球对杆的作用力大小为6N,方向竖直向上.
由v=ωr,ω相等,可知B球的速度为:vB=3vA=6m/s
对B球,根据牛顿第二定律得:F2-mg=m$\frac{{v}_{B}^{2}}{\frac{3}{4}L}$,
代入数据解得:F2=58N.
由牛顿第三定律得B球对杆的作用力大小为22N,方向竖直向下.
因此轴O所受的力大小为:FO=F2-F1=52N,方向竖直向下.
答:(1)vA=1.0m/s时,轴O所受的力大小为28N,方向竖直向下;
(2)vA=2.0m/s时,轴O所受的力大小为52N,方向竖直向下.
点评 本题关键要对两球分别受力分析,找出其向心力来源,根据牛顿第二定律列式求解,要注意在最高点,杆对A球的作用力方向可能向下,也可能向上,与A球的速度有关.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案 如图,R1和R2是材料相同、厚度相同、表面都为正方形的导体,R1的表面边长是R2的表面边长的2倍,则R1和R2的大小关系是( )
如图,R1和R2是材料相同、厚度相同、表面都为正方形的导体,R1的表面边长是R2的表面边长的2倍,则R1和R2的大小关系是( )| A. | R1>R2 | B. | R1=R2 | C. | R1<R2 | D. | 无法判断 |
| A. | mA=mB | B. | mA=$\frac{{m}_{B}}{2}$ | C. | mA=$\frac{{m}_{B}}{4}$ | D. | mA=$\frac{{m}_{B}}{8}$ |
 如图所示,小球用细绳悬挂于O点,在O点正下方有一固定的钉子C,把小球拉到水平位置后无初速释放,当细线转到竖直位置与钉子C相碰的前后瞬间,下列说法正确的为( )
如图所示,小球用细绳悬挂于O点,在O点正下方有一固定的钉子C,把小球拉到水平位置后无初速释放,当细线转到竖直位置与钉子C相碰的前后瞬间,下列说法正确的为( )| A. | 小球的线速度变大 | B. | 小球的向心加速度不变 | ||
| C. | 小球的向心加速度突然变大 | D. | 绳中张力突然变大 |
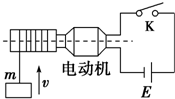 一台小型电动机在380V电压下正常工作时,能将30kg的货物在30s内匀速提升30m,通过它的电流是1A.除电动机线圈生热,其它能量损失不计,求在此过程中:
一台小型电动机在380V电压下正常工作时,能将30kg的货物在30s内匀速提升30m,通过它的电流是1A.除电动机线圈生热,其它能量损失不计,求在此过程中: 如图所示,物体A、B的质量分别为mA和mB,相互接触不粘连,它们与地面间动摩擦因数都为μ,物体A与弹簧右端相连,弹簧左端固定在墙上,现用手向左推动B使弹簧处于压缩状态,压缩量为x0,弹簧劲度系数为k,已知kx0>μ(mA+mB)g.
如图所示,物体A、B的质量分别为mA和mB,相互接触不粘连,它们与地面间动摩擦因数都为μ,物体A与弹簧右端相连,弹簧左端固定在墙上,现用手向左推动B使弹簧处于压缩状态,压缩量为x0,弹簧劲度系数为k,已知kx0>μ(mA+mB)g.
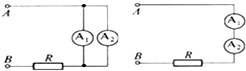 如图所示,A、B两点接在恒压电源上,内阻不可忽略的电流表并联,示数分别为2A和3A.若将两只电流表串联起来接入电路中,两只电流表的示数均为4A,那么电路不接入电流表时,流过R的电流是多少?
如图所示,A、B两点接在恒压电源上,内阻不可忽略的电流表并联,示数分别为2A和3A.若将两只电流表串联起来接入电路中,两只电流表的示数均为4A,那么电路不接入电流表时,流过R的电流是多少?