题目内容
7.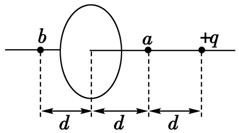 如图所示,有一带电量为+q的点电荷与均匀带电的圆形薄板相距为2d,圆形薄板带电量为-Q,点电荷到带电薄板的垂线通过板的圆心,若图中b点处的电场强度为零,则图中a点处的电场强度大小是( )
如图所示,有一带电量为+q的点电荷与均匀带电的圆形薄板相距为2d,圆形薄板带电量为-Q,点电荷到带电薄板的垂线通过板的圆心,若图中b点处的电场强度为零,则图中a点处的电场强度大小是( )| A. | $\frac{10kq}{9{d}^{2}}$ | B. | $\frac{8kq}{9{d}^{2}}$ | C. | $\frac{k(Q+q)}{{d}^{2}}$ | D. | $\frac{kq}{{d}^{2}}$ |
分析 据题,b点处的电场强度为零,+q与带电薄板在b点产生的场强大小相等,方向相反.+q在b处产生的场强大小为E=k$\frac{q}{{d}^{2}}$,得到带电薄板在b点产生的场强大小,根据对称性,确定带电薄板在a点产生的场强大小.+q在a处产生的场强大小为E=k$\frac{q}{(3d)^{2}}$,再根据叠加原理求解a点处的电场强度大小.
解答 解:+q在b处产生的场强大小为E=k$\frac{q}{{d}^{2}}$,方向水平向左.据题,b点处的电场强度为零,+q与带电薄板在b点产生的场强大小相等,方向相反,则带电薄板在b点产生的场强大小为E=k$\frac{q}{{d}^{2}}$,方向水平向右.
根据对称性可知,带电薄板在a点产生的场强大小为E=k$\frac{q}{{d}^{2}}$,方向水平向左.
+q在a处产生的场强大小为E=k$\frac{q}{(3d)^{2}}$,方向水平向左,
则a点处的电场强度大小是Ea=k$\frac{q}{(3d)^{2}}$+k$\frac{q}{{d}^{2}}$=$\frac{10kq}{9{d}^{2}}$,故A正确,BCD错误.
故选:A.
点评 本题考查电场的叠加,关键要抓住带电薄板产生的电场的对称性,并掌握点电荷电场强度公式的应用,注意矢量的方向性.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
17.一个电流表G,它的内阻是100Ω,满偏电流是2mA,若要把它改装成量程为1A的电流表.则电流表G应( )
| A. | 并联0.2Ω的电阻 | B. | 并联0.02Ω的电阻 | C. | 并联50Ω的电阻 | D. | 并联4900Ω的电阻 |
18.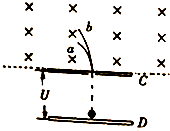 如图,一对水平放置的平行放置的平行金属板C、D始终与一直流电源两级相连,在C板上方存在一纸面向里的匀强磁场,在D板中央附近有一能发出a、b两种带电粒子的粒子源,而在C板上正对着粒子源处有一小孔,若a、b两种带电粒子经电场加速后,从C板上的小孔进入磁场的部分运动轨迹如图所示,则( )
如图,一对水平放置的平行放置的平行金属板C、D始终与一直流电源两级相连,在C板上方存在一纸面向里的匀强磁场,在D板中央附近有一能发出a、b两种带电粒子的粒子源,而在C板上正对着粒子源处有一小孔,若a、b两种带电粒子经电场加速后,从C板上的小孔进入磁场的部分运动轨迹如图所示,则( )
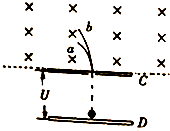 如图,一对水平放置的平行放置的平行金属板C、D始终与一直流电源两级相连,在C板上方存在一纸面向里的匀强磁场,在D板中央附近有一能发出a、b两种带电粒子的粒子源,而在C板上正对着粒子源处有一小孔,若a、b两种带电粒子经电场加速后,从C板上的小孔进入磁场的部分运动轨迹如图所示,则( )
如图,一对水平放置的平行放置的平行金属板C、D始终与一直流电源两级相连,在C板上方存在一纸面向里的匀强磁场,在D板中央附近有一能发出a、b两种带电粒子的粒子源,而在C板上正对着粒子源处有一小孔,若a、b两种带电粒子经电场加速后,从C板上的小孔进入磁场的部分运动轨迹如图所示,则( )| A. | C板一定与电源的正极相连 | |
| B. | 带电粒子a的比荷一定比带电粒子b的比荷大 | |
| C. | 在磁场中,带电粒子a一定的时间与带电粒子b一定的时间相等 | |
| D. | 带电粒子a进入磁场时的动能一定比带电粒子b进入磁场时的动能大 |
12.A、B两球在水平光滑轨道上同向运动,已知它们的动量分别是PA=5㎏•m/s,PB=7㎏•m/s.A从后面追上B并发生碰撞,碰后B球的动量变为10㎏•m/s.则两球质量mA、mB的关系中,下列哪个是可能的( )
| A. | mA=mB | B. | mA=$\frac{{m}_{B}}{2}$ | C. | mA=$\frac{{m}_{B}}{4}$ | D. | mA=$\frac{{m}_{B}}{8}$ |
16. 如图所示,小球用细绳悬挂于O点,在O点正下方有一固定的钉子C,把小球拉到水平位置后无初速释放,当细线转到竖直位置与钉子C相碰的前后瞬间,下列说法正确的为( )
如图所示,小球用细绳悬挂于O点,在O点正下方有一固定的钉子C,把小球拉到水平位置后无初速释放,当细线转到竖直位置与钉子C相碰的前后瞬间,下列说法正确的为( )
 如图所示,小球用细绳悬挂于O点,在O点正下方有一固定的钉子C,把小球拉到水平位置后无初速释放,当细线转到竖直位置与钉子C相碰的前后瞬间,下列说法正确的为( )
如图所示,小球用细绳悬挂于O点,在O点正下方有一固定的钉子C,把小球拉到水平位置后无初速释放,当细线转到竖直位置与钉子C相碰的前后瞬间,下列说法正确的为( )| A. | 小球的线速度变大 | B. | 小球的向心加速度不变 | ||
| C. | 小球的向心加速度突然变大 | D. | 绳中张力突然变大 |
17. 如图所示,质量为2m的木块A和质量为m的木块B之间用轻弹相连,在拉力F作用下,以加速度为g竖直向上做匀加速直线运动,某时刻突然撤去拉力F.此瞬间A和B的加速度大小为aA和aB,则( )
如图所示,质量为2m的木块A和质量为m的木块B之间用轻弹相连,在拉力F作用下,以加速度为g竖直向上做匀加速直线运动,某时刻突然撤去拉力F.此瞬间A和B的加速度大小为aA和aB,则( )
 如图所示,质量为2m的木块A和质量为m的木块B之间用轻弹相连,在拉力F作用下,以加速度为g竖直向上做匀加速直线运动,某时刻突然撤去拉力F.此瞬间A和B的加速度大小为aA和aB,则( )
如图所示,质量为2m的木块A和质量为m的木块B之间用轻弹相连,在拉力F作用下,以加速度为g竖直向上做匀加速直线运动,某时刻突然撤去拉力F.此瞬间A和B的加速度大小为aA和aB,则( )| A. | aA=aB=g | B. | aA=g,aB=5g | C. | aA=0,aB=3g | D. | aA=$\frac{g}{2}$,aB=4g |
 一台小型电动机在380V电压下正常工作时,能将30kg的货物在30s内匀速提升30m,通过它的电流是1A.除电动机线圈生热,其它能量损失不计,求在此过程中:
一台小型电动机在380V电压下正常工作时,能将30kg的货物在30s内匀速提升30m,通过它的电流是1A.除电动机线圈生热,其它能量损失不计,求在此过程中:
 如图所示,物体A、B的质量分别为mA和mB,相互接触不粘连,它们与地面间动摩擦因数都为μ,物体A与弹簧右端相连,弹簧左端固定在墙上,现用手向左推动B使弹簧处于压缩状态,压缩量为x0,弹簧劲度系数为k,已知kx0>μ(mA+mB)g.
如图所示,物体A、B的质量分别为mA和mB,相互接触不粘连,它们与地面间动摩擦因数都为μ,物体A与弹簧右端相连,弹簧左端固定在墙上,现用手向左推动B使弹簧处于压缩状态,压缩量为x0,弹簧劲度系数为k,已知kx0>μ(mA+mB)g.