题目内容
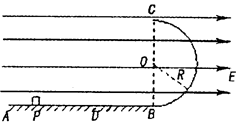
(16分)如图所示,让一可视为质点的小球从光滑曲面轨道上的A点无初速滑下,运动到轨道最低点B后,进入半径为R的光滑竖直圆轨道,并恰好通过轨道最高点C,离开圆轨道后继续在光滑平直轨道上运动到D点后抛出,最终撞击到搁在轨道末端点和水平地面之间的木板上,已知轨道末端点距离水平地面的高度为H=0.8m,木板与水平面间的夹角为θ=37°,小球质量为m=0.1kg,A点距离轨道末端竖直高度为h=0.2m,不计空气阻力。(取g=10m/s2,sin37°=0.6,cos37°=0.8)
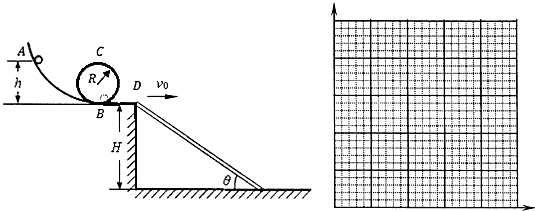
⑴求圆轨道半径R的大小;
⑵求小球从轨道末端点冲出后,第一次撞击木板时的位置距离木板上端的竖直高度有多大;
⑶若改变木板的长度,并使木板两端始终与平台和水平面相接,试通过计算推导小球第一次撞击木板时的动能随木板倾角θ变化的关系式,并在图中作出Ek-(tanθ)2图象。

⑴求圆轨道半径R的大小;
⑵求小球从轨道末端点冲出后,第一次撞击木板时的位置距离木板上端的竖直高度有多大;
⑶若改变木板的长度,并使木板两端始终与平台和水平面相接,试通过计算推导小球第一次撞击木板时的动能随木板倾角θ变化的关系式,并在图中作出Ek-(tanθ)2图象。
⑴R=0.08m;⑵y=0.45m;⑶Ek=0.8tan2θ+0.2,其中0<tan2θ≤1,


试题分析:⑴小球恰好能通过C点,因此,在C点,根据牛顿第二定律和向心力公式有:mg=
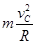
小球由A点运动至C点的过程中,只有重力做功,根据动能定理有:mg(h-2R)=
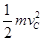 -0
-0联立以上两式解得:R=
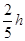 =0.08m
=0.08m⑵小球从A点运动至D点的过程中,只有重力做功,根据动能定理有:mgh=
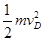 -0
-0小球离开D点后开始做平抛运动,设经时间t落到木板上,根据平抛运动规律可知,在水平方向上有:x=vDt
在竖直方向上有:y=
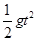
根据图中几何关系有:tanθ=
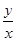
联立以上各式解得:y=4htan2θ=0.45m,即小球从轨道末端点冲出后,第一次撞击木板时的位置距离木板上端的竖直高度为:y=0.45m
⑶小球从离开D点到第一次撞击木板的过程中,根据动能定理有:mgy=Ek-
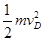
解得:Ek=mgy+
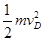
由⑵中求解可知:Ek=mgh(4tan2θ+1)=0.8tan2θ+0.2
显然,当小球落地时动能最大,为:Ekm=mg(h+H)=1J
所以有:0<tan2θ≤1,其图象如下图所示。


练习册系列答案
相关题目
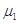 ,木块与长木板间动摩擦因数为
,木块与长木板间动摩擦因数为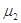 ,则滑行过程中木块受到的摩擦力一定为( )
,则滑行过程中木块受到的摩擦力一定为( )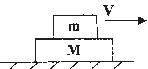
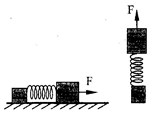
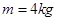 的物体,让其在随位移均匀减小的水平推力作用下运动,推力
的物体,让其在随位移均匀减小的水平推力作用下运动,推力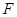 随位移
随位移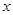 变化的图象如图乙所示。已知物体与地面之间的动摩擦因数为
变化的图象如图乙所示。已知物体与地面之间的动摩擦因数为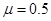 ,
,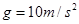 .求:
.求: