题目内容
(9分)如图,质量分别为 、
、 的两个小球A、B静止在地面上方,B球距地面的高度h=0.8m,A球在B球的正上方。 先将B球释放,经过一段时间后再将A球释放。 当A球下落t=0.3s时,刚好与B球在地面上方的P点处相碰,碰撞时间极短,碰后瞬间A球的速度恰为零。已知
的两个小球A、B静止在地面上方,B球距地面的高度h=0.8m,A球在B球的正上方。 先将B球释放,经过一段时间后再将A球释放。 当A球下落t=0.3s时,刚好与B球在地面上方的P点处相碰,碰撞时间极短,碰后瞬间A球的速度恰为零。已知 ,重力加速度大小为
,重力加速度大小为 ,忽略空气阻力及碰撞中的动能损失。
,忽略空气阻力及碰撞中的动能损失。 
(i)B球第一次到达地面时的速度;
(ii)P点距离地面的高度。


解析试题分析:(i)B球总地面上方静止释放后只有重力做功,根据动能定理有
可得B球第一次到达地面时的速度
(ii)A球下落过程,根据自由落体运动可得A球的速度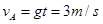
设B球的速度为 , 则有碰撞过程动量守恒
, 则有碰撞过程动量守恒
碰撞过程没有动能损失则有
解得 ,
,
小球B与地面碰撞后根据没有动能损失所以B离开地面上抛时速度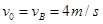
所以P点的高度
考点:动量守恒定律 能量守恒

练习册系列答案
相关题目
如图所示,传送带与地面的倾角θ,传送带以v匀速运动,在传送带底端无初速地放置一个质量为m的物体,当物体上升高度h时,物体已经相对传动带静止,在这个过程中分析正确的是( ) 
| A.动能增加mgh |
B.动能增加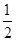 mv2 mv2 |
C.机械能增加 mgh-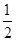 mv2 mv2 |
D.重力势能增加mgh+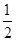 mv2 mv2 |




 (取无穷远处引力势能为零),其中m为此时“嫦娥三号”的质量。若“嫦娥三号”在轨道II上运动的过程中,动能和引力势能相互转化,它们的总量保持不变。已知“嫦娥三号”经过Q点的速度大小为v,请根据能量守恒定律求它经过P点时的速度大小;
(取无穷远处引力势能为零),其中m为此时“嫦娥三号”的质量。若“嫦娥三号”在轨道II上运动的过程中,动能和引力势能相互转化,它们的总量保持不变。已知“嫦娥三号”经过Q点的速度大小为v,请根据能量守恒定律求它经过P点时的速度大小;
 、固定于竖直平面内的
、固定于竖直平面内的 光滑圆弧轨道,轨道上端切线水平。PQ为待检验的固定曲面,该曲面为在竖直面内截面半径
光滑圆弧轨道,轨道上端切线水平。PQ为待检验的固定曲面,该曲面为在竖直面内截面半径 的
的 的小钢珠,假设某次发射的钢珠沿轨道恰好能经过N点,水平飞出后落到PQ上的S点,取g =10m/s2。求:
的小钢珠,假设某次发射的钢珠沿轨道恰好能经过N点,水平飞出后落到PQ上的S点,取g =10m/s2。求:
 的大小;
的大小; 的大小;
的大小; 的大小。
的大小。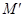 从右端滑上B,并以1/2
从右端滑上B,并以1/2 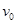 滑离B,恰好能到达C的最高点。A、B、C的质量均为m,试求:
滑离B,恰好能到达C的最高点。A、B、C的质量均为m,试求: