题目内容
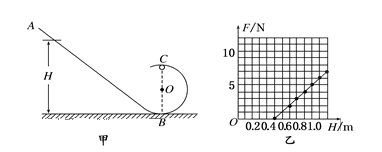
(13分)如图是检验某种防护罩承受冲击能力的装置,MN为半径 、固定于竖直平面内的
、固定于竖直平面内的 光滑圆弧轨道,轨道上端切线水平。PQ为待检验的固定曲面,该曲面为在竖直面内截面半径
光滑圆弧轨道,轨道上端切线水平。PQ为待检验的固定曲面,该曲面为在竖直面内截面半径 的
的 圆弧,圆弧下端切线水平且圆心恰好位于MN轨道的上端点N,M的下端相切处放置竖直向上的弹簧枪,可发射速度不同的质量
圆弧,圆弧下端切线水平且圆心恰好位于MN轨道的上端点N,M的下端相切处放置竖直向上的弹簧枪,可发射速度不同的质量 的小钢珠,假设某次发射的钢珠沿轨道恰好能经过N点,水平飞出后落到PQ上的S点,取g =10m/s2。求:
的小钢珠,假设某次发射的钢珠沿轨道恰好能经过N点,水平飞出后落到PQ上的S点,取g =10m/s2。求:
(1)小球到达N点时速度 的大小;
的大小;
(2)发射该钢珠前,弹簧的弹性势能 的大小;
的大小;
(3)钢珠落到圆弧PQ上S点时速度 的大小。
的大小。
(1)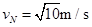 (2)
(2)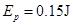 (3)
(3)
解析试题分析:(1)恰好能过N点,则在N点时重力充当向心力,所以根据牛顿第二定律可得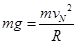 (2分)
(2分)
故解得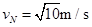 (1分)
(1分)
(2) 弹簧的弹性势能转化为动能和重力势能,所以有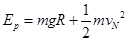 (2分)
(2分)
解得: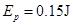 (1分)
(1分)
(3)从N点出来后,恰好做平抛运动,所以在水平方向上有: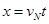 (1分)
(1分)
在竖直方向上有: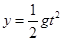 (1分)
(1分)
根据几何知识可得: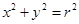 (1分)
(1分)
故解得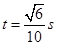 (1分)
(1分)
根据速度的合成可得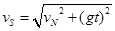 (2分)
(2分)
故 (1分)
(1分)
考点:考查了圆周运动,机械能守恒,平抛运动规律的综合应用

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
NBA篮球赛非常精彩,吸引了众多观众。经常有这样的场面:在临终场0.1s的时候,运动员把球投出且准确命中,获得比赛的胜利。如果运动员投篮过程中对篮球做功为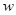 ,出手高度为h1,篮筐距地面高度为h2,篮球的质量为
,出手高度为h1,篮筐距地面高度为h2,篮球的质量为 ,空气阻力不计,则篮球进筐时的动能为
,空气阻力不计,则篮球进筐时的动能为
| A.W+mgh1-mgh2 | B.W+mgh2-mgh1 |
| C.mgh1+mgh2-W | D.mgh2-mgh1-W |
 、
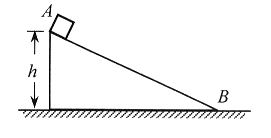
、 的两个小球A、B静止在地面上方,B球距地面的高度h=0.8m,A球在B球的正上方。 先将B球释放,经过一段时间后再将A球释放。 当A球下落t=0.3s时,刚好与B球在地面上方的P点处相碰,碰撞时间极短,碰后瞬间A球的速度恰为零。已知
的两个小球A、B静止在地面上方,B球距地面的高度h=0.8m,A球在B球的正上方。 先将B球释放,经过一段时间后再将A球释放。 当A球下落t=0.3s时,刚好与B球在地面上方的P点处相碰,碰撞时间极短,碰后瞬间A球的速度恰为零。已知 ,重力加速度大小为
,重力加速度大小为 ,忽略空气阻力及碰撞中的动能损失。
,忽略空气阻力及碰撞中的动能损失。 
 与滑块B发生碰撞(碰撞时间极短)后粘在一起,并压缩弹簧推动滑块C向前运动,经一段时间,滑块C脱离弹簧,继续在水平面上匀速运动,求:
与滑块B发生碰撞(碰撞时间极短)后粘在一起,并压缩弹簧推动滑块C向前运动,经一段时间,滑块C脱离弹簧,继续在水平面上匀速运动,求: