题目内容
8. 右图是一个十字路口的示意图,每条停车线到十字路中心O的距离均为20m.一人骑电动助力车以7m/s的速度到达停车线(图中A点)时,发现左前方道路一辆轿车正以8m/s的速度驶来,车头已抵达停车线(图中B),设两车均沿道路中央作直线运动,助力车可视为质点,轿车长4.8m,宽度可不计.
右图是一个十字路口的示意图,每条停车线到十字路中心O的距离均为20m.一人骑电动助力车以7m/s的速度到达停车线(图中A点)时,发现左前方道路一辆轿车正以8m/s的速度驶来,车头已抵达停车线(图中B),设两车均沿道路中央作直线运动,助力车可视为质点,轿车长4.8m,宽度可不计.(1)请通过计算判断两车保持上述速度匀速运动,是否会发生相 撞事故.
(2)若助力车保持上述速度匀速运动,而轿车立即作匀减速直线运动,为避免发生相撞事故,轿车的加速度至少要多大.
分析 (1)先求出轿车运动到o点的时间和通过o点的时间,再求出助力车运动到o的时间,比较两个时间的关系即可解题;
(2)设轿车的最小加速度am,在助力车匀速到达o点时刚好通过o点,根据运动学基本公式即可解题
解答 解:(1)轿车车头到达O点的时间为:
t1=$\frac{{x}_{1}}{{v}_{1}}$=$\frac{20}{8}$s=2.5s
轿车通过O点的时间为:
△t=$\frac{△x}{{v}_{1}}$=$\frac{4.8}{8}$s=0.6s
助力车到达O点的时间为:
t2=$\frac{{x}_{2}}{{v}_{2}}$=$\frac{20}{7}$s
因为 t1<t2<t1+△t,所以会发生交通事故
(2)若助力车保持上述速度匀速运动,到达中心线的时间为t=$\frac{20}{7}$s,轿车到达O点的时间大于t,可避免交通事故发生,设轿车的最小加速度大小为am,则与:
x1+△x=v1t2-$\frac{1}{2}$amt${\;}_{2}^{2}$
代入数据有:10+4.8=8×2-$\frac{1}{2}$×am×$(\frac{20}{7})$2
解得:am=4.68m/s2
答:(1)通过计算判断两车保持上述速度匀速运动,会发生相撞事故.
(2)若助力车保持上述速度匀速运动,而轿车立即作匀减速直线运动,为避免发生相撞事故,轿车的加速度至少要4.68m/s2
点评 本题考查了运动学基本公式的应用,注意抓住在运动过程中助力车与轿车的时间是相等的,根据运动学基本公式列式即可解题,难度适中.

练习册系列答案
相关题目
18. 一带负电的粒子只在电场力作用下沿x轴正向运动,其电势能EP随位移x变化的关系如图所示,其中0~x2段是对称的曲线,x2~x3段是直线,则下列说法正确的是( )
一带负电的粒子只在电场力作用下沿x轴正向运动,其电势能EP随位移x变化的关系如图所示,其中0~x2段是对称的曲线,x2~x3段是直线,则下列说法正确的是( )
 一带负电的粒子只在电场力作用下沿x轴正向运动,其电势能EP随位移x变化的关系如图所示,其中0~x2段是对称的曲线,x2~x3段是直线,则下列说法正确的是( )
一带负电的粒子只在电场力作用下沿x轴正向运动,其电势能EP随位移x变化的关系如图所示,其中0~x2段是对称的曲线,x2~x3段是直线,则下列说法正确的是( )| A. | x1处粒子的动能最小 | |
| B. | x1、x2、x3处电势φ1、φ2、φ3的关系为φ1>φ2>φ3 | |
| C. | 粒子在0~x2段做变速运动,x2~x3段做匀速运动 | |
| D. | x2~x3段不一定是匀强电场 |
19. 2010年10月,我国成功发射了“嫦娥二号”探月飞行器,它的工作轨道是距月球表面100km的圆形轨道,而当年我国的“嫦娥一号”绕月飞行器的工作圆轨道距月球表面约为200km(见图).则下列说法正确的是( )
2010年10月,我国成功发射了“嫦娥二号”探月飞行器,它的工作轨道是距月球表面100km的圆形轨道,而当年我国的“嫦娥一号”绕月飞行器的工作圆轨道距月球表面约为200km(见图).则下列说法正确的是( )
 2010年10月,我国成功发射了“嫦娥二号”探月飞行器,它的工作轨道是距月球表面100km的圆形轨道,而当年我国的“嫦娥一号”绕月飞行器的工作圆轨道距月球表面约为200km(见图).则下列说法正确的是( )
2010年10月,我国成功发射了“嫦娥二号”探月飞行器,它的工作轨道是距月球表面100km的圆形轨道,而当年我国的“嫦娥一号”绕月飞行器的工作圆轨道距月球表面约为200km(见图).则下列说法正确的是( )| A. | “嫦娥二号”比“嫦娥一号”在工作轨道上运行的速度更小 | |
| B. | “嫦娥二号”比“嫦娥一号”在工作轨道上运行的向心加速度更大 | |
| C. | “嫦娥二号”在绕月圆轨道上运行时须向运动的反方向喷气以提高速率 | |
| D. | 若已知“嫦娥二号”的转动周期和月球的半径,则利用题中提供的数据,可以求出月球表面的重力加速度 |
16. 蹦极是一项新兴的极限运动,跳跃者把一端固定的长弹性绳绑在踝关节等处,从几十米高处跳下,在弹性绳索的作用下反复下落、弹起.如图是某次蹦极下落过程的示意图,O点为弹性绳固定点,也是人的起跳点,A点是弹性绳刚被拉直时人的位置,B点是下落到达的最低点.下列说法中正确的是( )
蹦极是一项新兴的极限运动,跳跃者把一端固定的长弹性绳绑在踝关节等处,从几十米高处跳下,在弹性绳索的作用下反复下落、弹起.如图是某次蹦极下落过程的示意图,O点为弹性绳固定点,也是人的起跳点,A点是弹性绳刚被拉直时人的位置,B点是下落到达的最低点.下列说法中正确的是( )
 蹦极是一项新兴的极限运动,跳跃者把一端固定的长弹性绳绑在踝关节等处,从几十米高处跳下,在弹性绳索的作用下反复下落、弹起.如图是某次蹦极下落过程的示意图,O点为弹性绳固定点,也是人的起跳点,A点是弹性绳刚被拉直时人的位置,B点是下落到达的最低点.下列说法中正确的是( )
蹦极是一项新兴的极限运动,跳跃者把一端固定的长弹性绳绑在踝关节等处,从几十米高处跳下,在弹性绳索的作用下反复下落、弹起.如图是某次蹦极下落过程的示意图,O点为弹性绳固定点,也是人的起跳点,A点是弹性绳刚被拉直时人的位置,B点是下落到达的最低点.下列说法中正确的是( )| A. | OB过程中人下落至A点时速度最大 | B. | AB过程中人先加速后减速 | ||
| C. | AB过程中人的加速度先减小后增大 | D. | 人运动至B点时处于平衡状态 |
3. 如图所示为一与水平方向成夹角α的传送带.现将一质量为m的工件放在传送带上,此工件恰好随皮带以相同加速度a(a>gsinα)向下匀加速运动,则在工件运动过程中下列说法正确的是( )
如图所示为一与水平方向成夹角α的传送带.现将一质量为m的工件放在传送带上,此工件恰好随皮带以相同加速度a(a>gsinα)向下匀加速运动,则在工件运动过程中下列说法正确的是( )
 如图所示为一与水平方向成夹角α的传送带.现将一质量为m的工件放在传送带上,此工件恰好随皮带以相同加速度a(a>gsinα)向下匀加速运动,则在工件运动过程中下列说法正确的是( )
如图所示为一与水平方向成夹角α的传送带.现将一质量为m的工件放在传送带上,此工件恰好随皮带以相同加速度a(a>gsinα)向下匀加速运动,则在工件运动过程中下列说法正确的是( )| A. | 工件受到皮带的摩擦力沿斜面向上 | |
| B. | 摩擦力对工件一定做正功 | |
| C. | 皮带与工件的动摩擦因数一定大于tanα | |
| D. | 工件所受摩擦力的大小可能等于mgsinα |
13.以初速V0竖直上抛一个小球,若不计空气阻力,在上升过程中,从抛出到小球动能减少一半所经过的时间( )
| A. | $\frac{{v}_{0}}{g}$ | B. | $\frac{{v}_{0}}{2g}$ | C. | $\frac{\sqrt{2}{v}_{0}}{2g}$ | D. | $\frac{{v}_{0}}{g}$(1-$\frac{\sqrt{2}}{2}$) |
20.如图所示,三个相同的灯泡a、b、c和电阻不计的线圈L与内阻不计的电源连接,下列判断正确的有( )
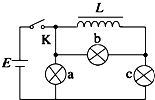

| A. | K闭合的瞬间,b、c两灯亮度不同 | |
| B. | K闭合的瞬间,a灯最亮 | |
| C. | K断开的瞬间,a、c两灯立即熄灭 | |
| D. | K断开之后,a、c两灯逐渐变暗且亮度相同 |
18.某物理兴趣小组的同学利用实验探究电池的电动势和内阻,实验的主要操作如下:
①先用电压表直接接在电池两极粗测电池的电动势,这样测出的电动势比真实值偏小(选填“偏大”或“偏小”).
②若按图(甲)所示接好电路进行实验,记下电阻箱和电压表对应的一系列读数R、U,并将数据记录在下表中.第2次实验中,电阻箱的示数如图(乙)所示,此时电阻箱接入电路的电阻是2Ω;

③图(丙)是根据上表中的数据,在坐标纸上画出的$\frac{1}{U}$-$\frac{1}{R}$图象.若忽略电压表内阻的影响,当电阻箱、电压表的示数分别是R、U时,电池电动势E=U+$\frac{U}{R}r$(用U、R、r表示);设$\frac{1}{U}$-$\frac{1}{R}$图象纵轴截距为A,则A与电池电动势E的函数关系式是$\frac{1}{E}$,该图象的斜率K与E、r之间的函数关系式是$\frac{r}{E}$;
④根据图象可知:电池的电动势E=1.67V,内阻r=1.34Ω.(结果保留三位有效数字)
①先用电压表直接接在电池两极粗测电池的电动势,这样测出的电动势比真实值偏小(选填“偏大”或“偏小”).
②若按图(甲)所示接好电路进行实验,记下电阻箱和电压表对应的一系列读数R、U,并将数据记录在下表中.第2次实验中,电阻箱的示数如图(乙)所示,此时电阻箱接入电路的电阻是2Ω;
| 实验次数 | 1 | 2 | 3 | 4 | 5 | 6 |
| $\frac{1}{U}$/(V-1) | 0.80 | 1.07 | 1.30 | 1.47 | 1.80 | 2.27 |
| $\frac{1}{R}$/(Ω-1) | 0.2 | 0.8 | 1.0 | 1.5 | 2.0 |

③图(丙)是根据上表中的数据,在坐标纸上画出的$\frac{1}{U}$-$\frac{1}{R}$图象.若忽略电压表内阻的影响,当电阻箱、电压表的示数分别是R、U时,电池电动势E=U+$\frac{U}{R}r$(用U、R、r表示);设$\frac{1}{U}$-$\frac{1}{R}$图象纵轴截距为A,则A与电池电动势E的函数关系式是$\frac{1}{E}$,该图象的斜率K与E、r之间的函数关系式是$\frac{r}{E}$;
④根据图象可知:电池的电动势E=1.67V,内阻r=1.34Ω.(结果保留三位有效数字)
 如图所示,甲船及人的总质量为m1,乙船及人的总质量为m2,已知m1=2m2,甲、乙两船上的人各拉着水平轻绳的一端对绳施力,设甲船上的人施力为F1,乙船上的人施力为F2.甲、乙两船原来都静止在水面上,不考虑水对船的阻力,甲船产生的加速度大小为a1,乙船产生的加速度大小为a2,则F1:F2,a1:a2各是多少?
如图所示,甲船及人的总质量为m1,乙船及人的总质量为m2,已知m1=2m2,甲、乙两船上的人各拉着水平轻绳的一端对绳施力,设甲船上的人施力为F1,乙船上的人施力为F2.甲、乙两船原来都静止在水面上,不考虑水对船的阻力,甲船产生的加速度大小为a1,乙船产生的加速度大小为a2,则F1:F2,a1:a2各是多少?