��Ŀ����
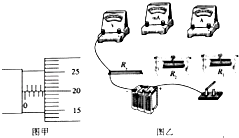
����Ŀ����ͼ��ʾ�������˷�մ�ϸ���ȵ���ֱ���ܵ��ڣ���һ�������ƶ��Ļ���A��������ȵ����������壮��ʼʱ�ܵ��������¶ȶ�ΪT0=500K���²��������ѹǿp0=1.25��105Pa����������m=0.25kg���ܵ����ھ�������S=1cm2 �� �ֱ��ֹܵ��²��������¶Ȳ��䣬�ϲ��������¶Ȼ�������T�����չܵ����ϲ������������Ϊԭ���� ![]() �������ƻ�����ܵ��ڼ��Ħ����g=10m/s2 �� ���ʱ�ϲ���������¶�T��
�������ƻ�����ܵ��ڼ��Ħ����g=10m/s2 �� ���ʱ�ϲ���������¶�T��![]()
���𰸡��⣺���״̬ʱ���������������ΪV0�����²������壬���±仯�����ݲ��������֪��P0V0=PV��
���� ![]()
��ã�P= ![]() 1.25��105Pa=1��l05Pa
1.25��105Pa=1��l05Pa
���ϲ������壬��̬��P1=P0�� ![]() =1��105Pa
=1��105Pa
ĩ̬�� ![]()
������������״̬���̣��У� ![]()
��ã�T=281.25 K
�𣺴�ʱ�ϲ���������¶�T=281.25 K��
�����������²����������֪����Ϊ���±仯�����ݲ���������������ѹǿ���ٸ���ƽ������ϲ�������ѹǿ�������ϲ���������ݸ�����������״̬������ʽ���¶ȣ�

��ϰ��ϵ�д�
 �±�Сѧ��Ԫ�Բ���ϵ�д�
�±�Сѧ��Ԫ�Բ���ϵ�д� �ִʾ��ƪϵ�д�
�ִʾ��ƪϵ�д�
�����Ŀ