��Ŀ����
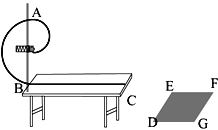
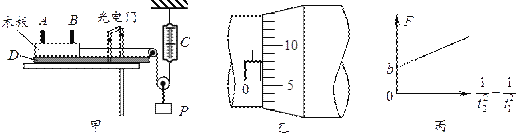
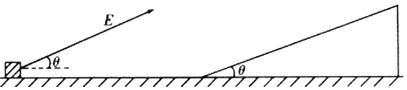
����Ŀ����ͼ��ʾ��һ����Ϊlkg���������Ϊ1.0��10-6C����龲ֹ�ڴֲڳ̶���ͬ�ľ�Եˮƽ���ϡ�t=0ʱ�̣���һб���ϡ���ˮƽ�������=37���ǵ��ޱ߽���ǿ�糡�����忪ʼ��ˮƽ�������˶���һ��ʱ������һ���ҲΪ�����㹻���⻬��Եб�棬�����������ˮƽ�浽б���������ʧ����t=0ʱ�̿�ʼ��ÿ��0.1sͨ���ٶȴ�������������˲ʱ�ٶȣ����ֲ����������±���ʾ����֪sin37��=06��g=10m/s2����
t/s | �� | 3.0 | �� | 4.2 | 4.3 | 4.4 | �� |
v/��m/s-1�� | �� | 3.9 | �� | 4.8 | 4.6 | 4.4 | �� |
(1)�糡ǿ�ȵĴ�С��
(2)�����ˮƽ���Ķ�Ħ��������
(3)������������߶ȣ����������λ��Ч���֣���
���𰸡�(1)![]() ��(2)0.25��(3)4.1m
��(2)0.25��(3)4.1m
��������
����б�����ȼ���ֱ���˶������ȼ��ٺ��ȼ����˶��ļ��ٶȷֱ�Ϊa1��a2��
�ɱ������ݿ�֪��![]() ��
��
![]() ��
��
�����б�������˶��Ĺ����У���ţ�ٵڶ����ɵã�
mgsin��-qE=ma2 ��
�������ݽ�ã�E=4��106V/m ��
��2�������ˮƽ���˶���������ţ�ٵڶ����ɵã�
qEcos��-��FN=ma1 ��
��ֱ��������ƽ��ã�
FN+qEsin��=mg ��
�٢ܢݢ�������ã���=0.25
��3����������ȼ����˶�ʱ��Ϊt������ٶ�Ϊv���������֪
v=a1t ��
4.8=v-a2��4.2-t����
�ߢ�������ã�t=4.0s
�������б���ϻ������߶�Ϊh���ɶ��ܶ����ã�
![]() ��
��
�������ݽ�ã�h=4.056m��4.1m