Question

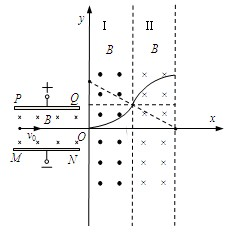
如图所示，带电平行金属板PQ和MN之间的距离为d，金属板之间有垂直纸面向外的匀强磁场，磁感应强度大小为B，x轴与金属板中心线重合，y轴垂直于金属板，在区域Ⅰ和区域Ⅱ内存在方向相同的匀强磁场，磁感应强度大小分别为B₁和B₂，且B₁＜B₂，一电子沿着x轴正向以速度v₀射入平行板之间，在平行板间恰好沿着x轴正方向做直线运动，并由区域Ⅰ进入区域Ⅱ，然后经过y轴离开区域Ⅰ，已知区域Ⅰ沿x轴方向宽度为

3 mv0

2B1e

，区域Ⅱ的宽度足够大，电子电荷量为e，质量为m，不计电子重力，求：
（1）两金属板之间电势差U；
（2）电子在区域Ⅰ和区域Ⅱ中运动的半径R₁和R₂；
（3）电子两次经过y轴的时间间隔t．

Answer 1

（1）粒子在板间做直线运动，则洛伦兹力和电场力相等：ev0B=e

U

d

得：U=Bv₀d
（2）粒子的轨迹如图，在区域I、II内，由qvB=m

v

R

得：
R1=

mv0

eB1

同理：R2=

mv0

eB2

（3）由几何关系可知：

L

R1

=sinθ1
得：θ₁=60°
θ₁=θ₂=60°
由：T=

2πR

v

得：T=

2πm

qB

则t1=

1

6

T1=

πm

3eB1

t2=

1

6

T2=

πm

3eB2

t=2t1+t2=

πm

3e

(

2

B1

+

1

B2

)
答：（1）两金属板之间电势差U为Bv₀d；
（2）电子在区域Ⅰ和区域Ⅱ中运动的半径R₁和R₂分别为

mv0

eB1

、

mv0

eB2

；
（3）电子两次经过y轴的时间间隔t为

πm

3e

（

2

B1

+

1

B2

）．