题目内容
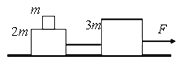
【题目】如图所示，在光滑的水平面上静止放一质量为m的“L”型木板B，木板表面光滑，左端固定一轻质弹簧，质量为2m的木块A以速度v0从板的右端水平向左滑上木板B，在木块A与弹簧相互作用的过程中，下列判断正确的是（ ）
A.弹簧压缩量最大时，B板运动速率最大
B.B板的加速度一直增大
C.弹簧给木块A的冲量大小为 
mv0
D.弹簧的最大弹性势能为 
mv02
【答案】C,D
【解析】解：A、在木块A与弹簧相互作用的过程中，从弹簧的压缩量达到最大到弹簧恢复原状的过程中，弹簧对木板B有向左的弹力，B板仍在加速，所以弹簧压缩量最大时，B板运动速率不是最大，当弹簧恢复原长时B板的速率最大，故A错误；
B、弹簧压缩量先增加后减小，弹簧对B板的弹力先增大后减小，故B板的加速度先增加后减小，故B错误；
C、设弹簧恢复原长时A与B的速度分别为v1和v2．
取向左为正方向，根据动量守恒定律，有：2mv0=2mv1+mv2①
根据机械能守恒定律，有： 
2mv02= 2mv12+ mv22②
解得：v1= 
v0，v2= 
v0．
对滑块A，根据动量定理，有：I=2mv1﹣2mv0=﹣ mv0（负号表示方向向右），故C正确；
D、当滑块与长木板速度相等时，弹簧的压缩量最大；
根据动量守恒定律，有：2mv0=（m+2m）v ③
系统机械能守恒，根据守恒定律，有：Ep= 2mv02﹣ （2m+m）v2④
由③④两式解得：Ep= mv02，故D正确；
故选：CD
【考点精析】认真审题，首先需要了解动量守恒定律(动量守恒定律成立的条件：系统不受外力或系统所受外力的合力为零；系统所受的外力的合力虽不为零，但系统外力比内力小得多；系统所受外力的合力虽不为零，但在某个方向上的分量为零，则在该方向上系统的总动量的分量保持不变)．
