题目内容
10．
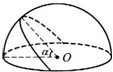如图所示，电荷均匀分布在半球面上，半球面上所有电荷在这半球的球心O处电场强度等于E．两个平面通过同一条直径，两平面之间的夹角为60°，从半球中分出一部分球面．则所分出的这部分球面上（在“小瓣”上）的电荷在球心O处产生的电场强度大小等于（ ）| A． | $\frac{{\sqrt{3}}}{2}E$ | B． | $\frac{E}{2}$ | C． | $\frac{E}{3}$ | D． | $\frac{E}{4}$ |
分析 半球的中心O处电场强度E0是部分球面上电荷产生的电场叠加的结果，根据对称性，作出球面上的电荷在O点产生的电场分布，由平行四边形定则求解“小瓣”球面上的电荷在O处的电场强度
解答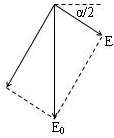 
解：根据对称性，作出球面上的电荷在O点产生的电场分布，如图所示，由平行四边形定则得到“小瓣”球面上的电荷在O处的电场强度E=E0sin$\frac{α}{2}$=$\frac{1}{2}$E0．
故选：B
点评 本题解题关键是抓住对称性，作出两部分球面上电荷产生的电场分布图．
练习册系列答案
相关题目
17．铁道转弯处内、外铁轨间设计有高度差，可以使火车顺利转弯，下列说法中正确的是（ ）
| A． | 主要是为了减少车轮与铁轨间的摩擦 | |
| B． | 主要是为了减少轮缘与铁轨间的挤压 | |
| C． | 内轨应略高于外轨 | |
| D． | 重力和支持力的合力为火车转弯提供了向心力 |
18．
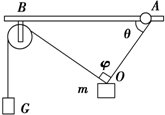如图所示，圆环套在水平棒上可以滑动，轻绳OA的A端与圆环套（重力不计）相连，O端与质量m=1kg的重物相连；定滑轮固定在B处，跨过定滑轮的轻绳，两端分别与重物m、重物G相连，当两条细绳间的夹角φ=90°，OA与水平杆的夹角θ=53°时圆环恰好没有滑动，不计滑轮大小，整个系统处于静止状态，已知sin 53°=0.8；cos 53°=0.6，滑动摩擦力等于最大静摩擦力．则下列说法正确的是（ ）
如图所示，圆环套在水平棒上可以滑动，轻绳OA的A端与圆环套（重力不计）相连，O端与质量m=1kg的重物相连；定滑轮固定在B处，跨过定滑轮的轻绳，两端分别与重物m、重物G相连，当两条细绳间的夹角φ=90°，OA与水平杆的夹角θ=53°时圆环恰好没有滑动，不计滑轮大小，整个系统处于静止状态，已知sin 53°=0.8；cos 53°=0.6，滑动摩擦力等于最大静摩擦力．则下列说法正确的是（ ）| A． | 圆环与棒间的动摩擦因数μ=0.75 | B． | 棒对环的支持力为1.6 N | ||
| C． | 重物G的质量M=0.6 kg | D． | 圆环与棒间的动摩擦因数μ=0.6 |
15．关于多用电表面板上的刻度线，下列说法中正确的是（ ）
| A． | 直流电流刻度线和直流电压刻度线都是均匀的，可共用同一刻度线 | |
| B． | 电阻刻度线是均匀的，且每一档的测量范围都是从0～∞ | |
| C． | 交流电压刻度线是均匀的 | |
| D． | 电阻刻度线上的零欧姆刻度线与直流电流刻度的最大刻度线相对应 |
