题目内容
5.一湖的南北两岸各有-码头A和B,有甲、乙两船分别于AB间往返穿梭匀速航行,且船每到一码头立即返航(不计船在码头停靠的间).某刻,甲和乙刚好分别自A和B出发,此后,两船的第一次相遇距A点300米,第二次相遇距B点200米,求湖宽多少?自第一相遇后,甲船至少还要航行多少米,这两船才会在第一次相遇的位置同样地相遇.分析 据两次相遇用位移关系列出方程联合求解湖宽;再利用两船的速度与胡宽列出两船同时到达AB两岸的路程关系,再据题意求出两船所走的趟数关系即可求解.
解答 解:设湖宽为L,甲乙两船的速度分别为v1、v2
设第一次相遇的时间为t,所以:
v1t=300 ①
v1t+v2t=L ②
联立①②得:$\frac{{v}_{1}}{{v}_{1}+{v}_{2}}$=$\frac{300}{L}$ ③
同理第二次相遇可推导出:$\frac{{v}_{1}}{{v}_{1}+{v}_{2}}$=$\frac{200+L}{3L}$ ④
联立③④解得:L=700m
$\frac{{v}_{1}}{{v}_{2}}$=$\frac{3}{4}$ ⑤
由于两船在第一次相遇的位置同样地相遇,所以两船应同时到达两岸(甲和乙刚好分别自A和B出发),设甲、乙两船同时到达两岸所用的时间为t1,所走的趟数分别为n、m(为整数)
所以:v1t1=700n ⑥
v2t2=700m ⑦
联立⑤⑥⑦得:$\frac{n}{m}$=$\frac{3}{4}$
两船应同时到达两岸(甲和乙刚好分别自A和B出发),所以n=6;m=8,才能保证回到原岸.
所以甲船至少再行驶的距离:s=6L-300m+300m=4200m
答:湖宽700m,自第一相遇后,甲船至少还要航行4200米,这两船才会在第一次相遇的位置同样地相遇.
点评 本题难度较大,一是需要明确运动示意图,找出各量间的关系,特别是理解好两船两船在第一次相遇的位置同样地相遇,否则易出现少或多300m的情况;二是所列方程的数据处理,否则易出现无法求解现象.

练习册系列答案
相关题目
12. 如图,两个质量均为m的小木块a和b(可视为质点)放在水平圆盘上,a与转轴的距离为l,b与转轴的距离为2l,a和b跟随圆盘以角速度ω绕OO'转动,下列说法正确的是( )
如图,两个质量均为m的小木块a和b(可视为质点)放在水平圆盘上,a与转轴的距离为l,b与转轴的距离为2l,a和b跟随圆盘以角速度ω绕OO'转动,下列说法正确的是( )
 如图,两个质量均为m的小木块a和b(可视为质点)放在水平圆盘上,a与转轴的距离为l,b与转轴的距离为2l,a和b跟随圆盘以角速度ω绕OO'转动,下列说法正确的是( )
如图,两个质量均为m的小木块a和b(可视为质点)放在水平圆盘上,a与转轴的距离为l,b与转轴的距离为2l,a和b跟随圆盘以角速度ω绕OO'转动,下列说法正确的是( )| A. | a、b的向心加速度 aa=2ab | B. | a、b的转动周期Tb=2Ta | ||
| C. | a、b的线速度 vb=2va | D. | a、b所受的静摩擦力Fa=Fb |
13. 电梯在t=0时由静止开始上升,运动的a-t图象如图所示(选取向上为正),电梯内乘客的质量m0=50kg,重力加速度g取10m/s2.下列说法正确的是( )
电梯在t=0时由静止开始上升,运动的a-t图象如图所示(选取向上为正),电梯内乘客的质量m0=50kg,重力加速度g取10m/s2.下列说法正确的是( )
 电梯在t=0时由静止开始上升,运动的a-t图象如图所示(选取向上为正),电梯内乘客的质量m0=50kg,重力加速度g取10m/s2.下列说法正确的是( )
电梯在t=0时由静止开始上升,运动的a-t图象如图所示(选取向上为正),电梯内乘客的质量m0=50kg,重力加速度g取10m/s2.下列说法正确的是( )| A. | 第9s内乘客处于失重状态 | |
| B. | 1~8s内乘客处于平衡状态 | |
| C. | 第2s内乘客对电梯的压力大小为550N | |
| D. | 第9s内电梯速度的增加量为1m/s |
17.在日常生活及各项体育运动中,有弹力出现的情况比较普遍,下列说法正确的是( )
| A. | 网球训练中击出的球撞击墙面弹回,是由于球发生弹性形变造成的 | |
| B. | 跳水运动中,运动员受到的支持力是跳板发生弹性形变而产生的 | |
| C. | 甲乙丙三位同学一字排开站立,甲同学用力推乙同学,结果乙同学没有倒,丙同学倒地,之所以丙同学会倒地,是因为甲同学对其施加了弹力的结果 | |
| D. | 小孩玩的弹弓之所以将弹丸能够弹出,是由于人对弹丸施加了弹力的结果 |
10.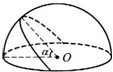 如图所示,电荷均匀分布在半球面上,半球面上所有电荷在这半球的球心O处电场强度等于E.两个平面通过同一条直径,两平面之间的夹角为60°,从半球中分出一部分球面.则所分出的这部分球面上(在“小瓣”上)的电荷在球心O处产生的电场强度大小等于( )
如图所示,电荷均匀分布在半球面上,半球面上所有电荷在这半球的球心O处电场强度等于E.两个平面通过同一条直径,两平面之间的夹角为60°,从半球中分出一部分球面.则所分出的这部分球面上(在“小瓣”上)的电荷在球心O处产生的电场强度大小等于( )
 如图所示,电荷均匀分布在半球面上,半球面上所有电荷在这半球的球心O处电场强度等于E.两个平面通过同一条直径,两平面之间的夹角为60°,从半球中分出一部分球面.则所分出的这部分球面上(在“小瓣”上)的电荷在球心O处产生的电场强度大小等于( )
如图所示,电荷均匀分布在半球面上,半球面上所有电荷在这半球的球心O处电场强度等于E.两个平面通过同一条直径,两平面之间的夹角为60°,从半球中分出一部分球面.则所分出的这部分球面上(在“小瓣”上)的电荷在球心O处产生的电场强度大小等于( )| A. | $\frac{{\sqrt{3}}}{2}E$ | B. | $\frac{E}{2}$ | C. | $\frac{E}{3}$ | D. | $\frac{E}{4}$ |
15.下列说法错误的是( )
| A. | 电源外部存在着由正极指向负极的电场,内部存在着由负极指向正极的电场 | |
| B. | 在电源外部电路中,负电荷靠静电力由电源的负极流向正极 | |
| C. | 在电源内部电路中,正电荷靠非静电力由电源的负极流向正极 | |
| D. | 在电池中,靠化学作用使化学能转化为电势能 |


 (1)如图所示是常用电器中电源的滤波装置,当输入端含有直流成分、交流高频成分和低频交流成分的电流时,能在输出端得到较稳定的直流电.L的作用为通直流、阻交流,通低频,阻高频;C1在此的功能为通交流,隔直流;C2在此的功能为通高频,阻低频.
(1)如图所示是常用电器中电源的滤波装置,当输入端含有直流成分、交流高频成分和低频交流成分的电流时,能在输出端得到较稳定的直流电.L的作用为通直流、阻交流,通低频,阻高频;C1在此的功能为通交流,隔直流;C2在此的功能为通高频,阻低频.