题目内容
2.利用打点计时器“探究小车的速度随时间变化的规律”,如图给出了某次实验中的纸带,其中0、1、2、3、5、6都为计数点,每相邻两个计数点的中间还有四点(未画出),从纸带上测得:s1=1.50cm,s2=2.00cm,s3=2.50cm,s4=3.00cm,s5=4.00cm,s6=5.00cm.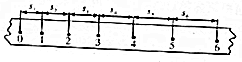
(1)通过纸带分析可知,小车的速度在增大(填“增大”或“减小”).
(2)每相邻两个计数点的时间间隔是0.1s.
(3)计数点4的瞬时速度是0.35m/s.(保留两位有效数字)
分析 根据相等时间内的位移变化判断小车的速度变化.根据打点的时间间隔,抓住相邻两个计数点的中间还有四点(未画出),求出相邻计数点间的时间间隔.
根据某段时间内的平均速度等于中间时刻的瞬时速度求出计数点4的瞬时速度.
解答 解:(1)因为相等时间内的位移逐渐增大,可知小车的速度在增大.
(2)打点计时器的打点周期为0.02s,每相邻两个计数点的中间还有四点(未画出),则相邻计数点间的时间间隔为0.1s.
(3)计数点4的瞬时速度的等于3、5两点间的平均速度,则有:${v}_{4}=\frac{{s}_{4}+{s}_{5}}{2T}=\frac{7×1{0}^{-2}}{0.2}m/s$=0.35m/s.
故答案为:(1)增大;(2)0.1;(3)0.35
点评 解决本题的关键掌握纸带的处理方法,会通过纸带求解瞬时速度和加速度,关键是匀变速直线运动推论的运用.注意有效数字的保留.

练习册系列答案
相关题目
9. 如图所示,在倾角为α的斜面上,一重为G的小球被竖直的木板挡住,不计一切摩擦,则小球对木板(挡板)的压力F1和对斜面的压力F2,的大小分别是( )
如图所示,在倾角为α的斜面上,一重为G的小球被竖直的木板挡住,不计一切摩擦,则小球对木板(挡板)的压力F1和对斜面的压力F2,的大小分别是( )
 如图所示,在倾角为α的斜面上,一重为G的小球被竖直的木板挡住,不计一切摩擦,则小球对木板(挡板)的压力F1和对斜面的压力F2,的大小分别是( )
如图所示,在倾角为α的斜面上,一重为G的小球被竖直的木板挡住,不计一切摩擦,则小球对木板(挡板)的压力F1和对斜面的压力F2,的大小分别是( )| A. | F1=Gsinα;F2=Gcosα | B. | F1=Gcosα;F2=Gsinα | ||
| C. | F1=Gtanα;${F_2}=\frac{G}{cosα}$ | D. | ${F_1}=\frac{G}{cosα}$;F2=Gtanα |
10.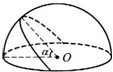 如图所示,电荷均匀分布在半球面上,半球面上所有电荷在这半球的球心O处电场强度等于E.两个平面通过同一条直径,两平面之间的夹角为60°,从半球中分出一部分球面.则所分出的这部分球面上(在“小瓣”上)的电荷在球心O处产生的电场强度大小等于( )
如图所示,电荷均匀分布在半球面上,半球面上所有电荷在这半球的球心O处电场强度等于E.两个平面通过同一条直径,两平面之间的夹角为60°,从半球中分出一部分球面.则所分出的这部分球面上(在“小瓣”上)的电荷在球心O处产生的电场强度大小等于( )
 如图所示,电荷均匀分布在半球面上,半球面上所有电荷在这半球的球心O处电场强度等于E.两个平面通过同一条直径,两平面之间的夹角为60°,从半球中分出一部分球面.则所分出的这部分球面上(在“小瓣”上)的电荷在球心O处产生的电场强度大小等于( )
如图所示,电荷均匀分布在半球面上,半球面上所有电荷在这半球的球心O处电场强度等于E.两个平面通过同一条直径,两平面之间的夹角为60°,从半球中分出一部分球面.则所分出的这部分球面上(在“小瓣”上)的电荷在球心O处产生的电场强度大小等于( )| A. | $\frac{{\sqrt{3}}}{2}E$ | B. | $\frac{E}{2}$ | C. | $\frac{E}{3}$ | D. | $\frac{E}{4}$ |
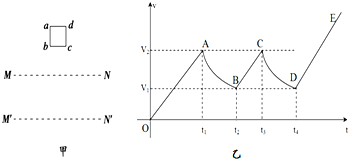
7.如图甲所示,abcd是位于竖直平面内的正方形闭合金属线框,在金属线框的下方有一磁感应强度为B的匀强磁场区域,MN和M′N′是匀强磁场区域的水平边界,边界的宽度为S,并与线框的bc边平行,磁场方向与线框平面垂直.现让金属线框由距MN的某一高度从静止开始下落,图乙是金属线框由开始下落到完全穿过匀强磁场区域的v-t图象(其中OA、BC、DE相互平行).已知金属线框的边长为L(L<S)、质量为m,电阻为R,当地的重力加速度为g,图象中坐标轴上所标出的字母v1、v2、t1、t2、t3、t4均为已知量,下落过程中bc边始终水平.根据题中所给条件,以下说法正确的是( )

| A. | t2是线框全部进入磁场瞬间,t4是线框全部离开磁场瞬间 | |
| B. | 从bc边进入磁场起一直到ad边离开磁场为止,感应电流所做的功为mgS | |
| C. | v1的大小可能为$\frac{mgR}{{{B^2}{L^2}}}$ | |
| D. | 线框穿出磁场过程中流经线框横截面的电荷量比线框进入磁场过程中流经框横截面的电荷量多 |
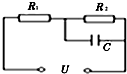
12.在图所示的电路中,U=8V不变,电容器电容C=2μF,R1:R2=3:5,则电容器带的电量为( )

| A. | 1×10-2C | B. | 1×10-5C | C. | 6×10-4C | D. | 1.6×10-3C |


 (1)如图所示是常用电器中电源的滤波装置,当输入端含有直流成分、交流高频成分和低频交流成分的电流时,能在输出端得到较稳定的直流电.L的作用为通直流、阻交流,通低频,阻高频;C1在此的功能为通交流,隔直流;C2在此的功能为通高频,阻低频.
(1)如图所示是常用电器中电源的滤波装置,当输入端含有直流成分、交流高频成分和低频交流成分的电流时,能在输出端得到较稳定的直流电.L的作用为通直流、阻交流,通低频,阻高频;C1在此的功能为通交流,隔直流;C2在此的功能为通高频,阻低频.