��Ŀ����
����Ŀ����ͼ��ʾ��һ����������Ϊm��2.0��10��11kg�������q��+1.0��10��5C���Ӿ�ֹ��ʼ����ѹΪU1��100V�ĵ糡���ٺ�ˮƽ������ƽ�н�������ƫת�糡�У�������糡ʱ��ƫת���ȣ�30���������Ž���һ������ֱֽ���������ΪD��34.6cm����ǿ�ų�������֪ƫת�糡�н����峤L��20cm��������d��17.3cm���������Բ��ƣ���
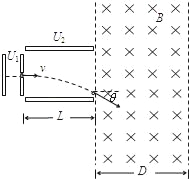
��1������������ƫת�糡ʱ������v1��
��2��ƫת�糡�����������ĵ�ѹU2��
��3��Ϊʹ�����������ɴų��ұ����������ǿ�ų��ĴŸ�Ӧǿ��B���ٶ��
���𰸡�(1)1.0��104m/s (2)66.7 V (3)0.1 T
��������
����(1)�����������ٵ糡���ٺ�����Ϊv1�����ݶ��ܶ�����U1q��![]() m
m![]()
v1����1.0��104m/s.
(2)��������ƫת�糡��ֻ�ܵ糡�����ã���������ų�ʱ���ٶ�Ϊv������
v����![]()
�ó�v����![]() v1.
v1.
�ɶ��ܶ�����
![]() m(v��2��v
m(v��2��v![]() )��q
)��q![]()
���U2��66.7 V.
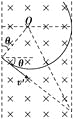
(3)����������ų�������Բ���˶������������ṩ������������ǡ�ò��Ӵų��ұ����ʱ��������Բ���˶��Ĺ���뾶ΪR���ɼ��ι�ϵ֪
R��![]() ��D
��D
��ţ���˶����ɼ��˶�ѧ����
qv��B��![]() ��
��
��B��0.1 T.
���������Ӳ�����ų����Ÿ�Ӧǿ��B����Ϊ0.1 T.

 ��У����ϵ�д�
��У����ϵ�д�