��Ŀ����
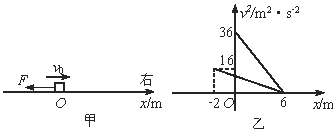
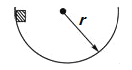
����Ŀ����ͼ��ʾ��ת̨�Ϲ̶���һ��Ϊ4L��ˮƽ�⻬ϸ�ˣ����������п�С��A��B��ϸ�˴�������ԭ��ΪL ���ᵯ������������С��A��B�������ֱ�Ϊ3m��2m.��ֱת�ᴦ��ת̨��ϸ�˵����������ϣ���ת̨��ת������ת��ʱ�� ��
A. ������ٶ�������С��B�ȽӴ�ת̨����
B. С��A.B�ܵ���������֮��Ϊ3��2
C. ���ᵯ�ɳ��ȱ�Ϊ2Lʱ��С��A��Բ���˶��İ뾶Ϊ1.2L
D. ���ᵯ�ɳ��ȱ�Ϊ3Lʱ��ת̨ת���Ľ��ٶ�Ϊ�����ɵľ���ϵ��Ϊ1.8m��
���𰸡�AD
��������
����С����ˮƽ����������Բ���˶��Ĺ����У�������Ҫ�����������ǵ��ɵĵ����ṩ�ġ����ݵ��ɵ������ص��֪��������Ҫ��������һ������ȵ�����B������һ��������Բ���˶����������ǵĽ��ٶ�����ȵġ������������Ĺ�ʽ�ɵã�3m��2r1��2m��2r2���֣�r1+r2=2L�������ɵã�r1��0.8L��r2��1.2L����C���������ϵķ����Ľ����֪��ֻҪ�Ƕ���һ��������Բ���˶�����B��ת��ľ���ʼ�մ���A��ת��ľ��룬����������ٶȣ�С��B�ȽӴ�ת̨��������A��ȷ�����ᵯ�ɳ��ȱ�Ϊ3Lʱ����r1+r2=3L��k(3LL)��3m��2r1��2m��2r2�������ɵõ��ɵľ���ϵ����k=1.8m��2����D��ȷ����ѡAD��