【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费
的包裹收费![]() 元;重量超过
元;重量超过![]() 的包裹,除
的包裹,除![]() 收费
收费![]() 元之外,超过
元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 计算)需再收
计算)需再收![]() 元.该公司将最近承揽的
元.该公司将最近承揽的![]() 件包裹的重量统计如下:
件包裹的重量统计如下:
包裹重量(单位: |
|
|
|
|
|
包裹件数 |
|
|
|
|
|
公司对近![]() 天,每天揽件数量统计如下表:
天,每天揽件数量统计如下表:
包裹件数范围 |
|
|
|
|
|
包裹件数 (近似处理) |
|
|
|
|
|
天数 |
|
|
|
|
|
以上数据已做近似处理,并将频率视为概率.
(1)计算该公司未来![]() 天内恰有
天内恰有![]() 天揽件数在
天揽件数在![]() 之间的概率;
之间的概率;
(2)(i)估计该公司对每件包裹收取的快递费的平均值;
(ii)公司将快递费的三分之一作为前台工作人员的工资和公司利润,剩余的用作其他费用.目前前台有工作人员![]() 人,每人每天揽件不超过
人,每人每天揽件不超过![]() 件,工资
件,工资![]() 元.公司正在考虑是否将前台工作人员裁减
元.公司正在考虑是否将前台工作人员裁减![]() 人,试计算裁员前后公司每日利润的数学期望,并判断裁员是否对提高公司利润更有利?
人,试计算裁员前后公司每日利润的数学期望,并判断裁员是否对提高公司利润更有利?
【题目】网购已经成为一种新型的购物方式,2018年天猫双11,仅1小时47分钟成交额超过1000亿元,比2017年达到1000亿元的时间缩短了7个小时,为了研究市民对网购的依赖性,从A城市16﹣59岁人群中抽取一个容量为100的样本,得出下列2×2列联表,其中16﹣39岁为青年,40﹣59岁为中年,当日消费金额超过1000元为消费依赖网购,否则为消费不依赖网购.
依赖网购 | 不依赖网购 | 小计 | |
青年(16﹣39岁) | 40 | 20 | |
中年(40﹣59岁) | 20 | 20 | |
小计 |
(1)完成2×2列联表,计算X2值,并判断是否有95%的把握认为网购依赖和年龄有关?
(2)把样本中的频率当作概率,随机从A城市中选取5人,其中依赖网购的人数为随机变量X,求随机变量X的分布列及期望(附:X2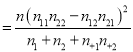 ,当X2>3.841时,有95%的把握说事件A与B有关,当X2≤3.841时,没有95%的把握说事件A与B有关)
,当X2>3.841时,有95%的把握说事件A与B有关,当X2≤3.841时,没有95%的把握说事件A与B有关)