【题目】某公司的甲、乙两名工程师因为工作需要,各自选购一台笔记本电脑.该公司提供了![]() 三款笔记本电脑作为备选,这三款笔记本电脑在某电商平台的销量和用户评分如下表所示:
三款笔记本电脑作为备选,这三款笔记本电脑在某电商平台的销量和用户评分如下表所示:
型号 |
|
|
|
销量(台) | 2000 | 2000 | 4000 |
用户评分 | 8 | 6.5 | 9.5 |
若甲选购某款笔记本电脑的概率与对应的销量成正比,乙选购某款笔记本电脑的概率与对应的用户评分减去5的值成正比,且他们两人选购笔记本电脑互不影响.
(1)求甲、乙两人选购不同款笔记本电脑的概率;
(2)若公司给购买这三款笔记本电脑的员工一定的补贴,补贴标准如下表:
型号 |
|
|
|
补贴(千元) | 3 | 4 | 5 |
记甲、乙两人获得的公司补贴之和为![]() 千元,求
千元,求![]() 的分布列和数学期望.
的分布列和数学期望.
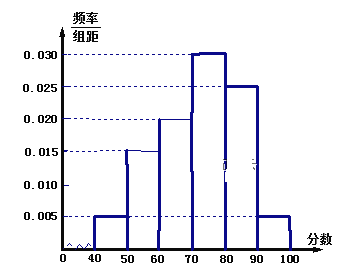
【题目】在考察疫情防控工作中,某区卫生防控中心提出了“要坚持开展爱国卫生运动,从人居环境改善、饮食习惯、社会心理健康、公共卫生设施等多个方面开展,特别是要坚决杜绝食用野生动物的陋习,提倡文明健康、绿色环保的生活方式”的要求.某小组通过问卷调查,随机收集了该区居民六类日常生活习惯的有关数据.六类习惯是:(1)卫生习惯状况类;(2)垃圾处理状况类;(3)体育锻炼状况类;(4)心理健康状况类;(5)膳食合理状况类;(6)作息规律状况类.经过数据整理,得到下表:
卫生习惯状况类 | 垃圾处理状况类 | 体育锻炼状况类 | 心理健康状况类 | 膳食合理状况类 | 作息规律状况类 | |
有效答卷份数 | 380 | 550 | 330 | 410 | 400 | 430 |
习惯良好频率 | 0.6 | 0.9 | 0.8 | 0.7 | 0.65 | 0.6 |
假设每份调查问卷只调查上述六类状况之一,各类调查是否达到良好标准相互独立.
(1)从小组收集的有效答卷中随机选取1份,求这份试卷的调查结果是膳食合理状况类中习惯良好者的概率;
(2)从该区任选一位居民,试估计他在“卫生习惯状况类、体育锻炼状况类、膳食合理状况类”三类习惯方面,至少具备两类良好习惯的概率;
(3)利用上述六类习惯调查的排序,用“![]() ”表示任选一位第k类受访者是习惯良好者,“
”表示任选一位第k类受访者是习惯良好者,“![]() ”表示任选一位第k类受访者不是习惯良好者(
”表示任选一位第k类受访者不是习惯良好者(![]() ).写出方差
).写出方差![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的大小关系.
的大小关系.