【题目】郑汴一体化是依托郑州省会城市资源优势发展开封的省级战略,实施至今,取得了一系列的成就:两城电信同价,金融同城,郑开大道全线贯通,城际列车实常态化运营.随着郑汴一体化的深入推进,很多人认为郑州开封未来有望合并.为了解市民对郑汴合并的态度,现随机抽查55人,结果按年龄分类统计形成如下表格:
支持 | 反对 | 合计 | |
不足35岁 | 20 | ||
35岁以上 | 30 | ||
合计 | 25 | 55 |
(1)请完成上面的2×2列联表,并判断是否有99.5%的把握认为市民对郑汴合并的态度与年龄有关?
(2)在上述样木中用分层抽样的方法,从攴持郑汴合并的两组市民中随机抽取6人作进一步调查,从这6人中任选2人,求恰有1位“不足35岁”的市民和1位“35岁及以上”的市民的概率.
附:![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.814 | 5.024 | 7.879 | 10.828 |
【题目】中国神舟十一号载人飞船在酒泉卫星发射中心成功发射,引起全国轰动.开学后,某校高二年级班主任对该班进行了一次调查,发现全班60名同学中,对此事关注的占![]() ,他们在本学期期末考试中的物理成绩(满分100分)如下面的频率分布直方图:
,他们在本学期期末考试中的物理成绩(满分100分)如下面的频率分布直方图:

(1)求“对此事关注”的同学的物理期末平均分(以各区间的中点代表该区间的均值).
(2)若物理成绩不低于80分的为优秀,请以是否优秀为分类变量,
①补充下面的![]() 列联表:
列联表:
物理成绩优秀 | 物理成绩不优秀 | 合计 | |
对此事关注 | |||
对此事不关注 | |||
合计 |
②是否有![]() 以上的把握认为“对此事是否关注”与物理期末成绩是否优秀有关系?
以上的把握认为“对此事是否关注”与物理期末成绩是否优秀有关系?
参考公式:  ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水库年入流量![]() (年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(1)求未来4年中,至多1年的年入流量超过120的概率;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量![]() 限制,并有如下关系:
限制,并有如下关系:
年入流量 |
|
|
|
发电量最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行,则该台年利润为5000万元;若某台发电机未运行,则该台年亏损800万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
【题目】某部门经统计,客户对不同款型理财产品的最满意程度百分比和对应的理财总销售量(万元)如下表(最满意度百分比超高时总销售量最高):
产品款型 | A | B | C | D | E | F | G | H | I | J |
最满意度% | 20 | 34 | 25 | 19 | 26 | 20 | 19 | 24 | 19 | 13 |
总销量(万元) | 80 | 89 | 89 | 78 | 75 | 71 | 65 | 62 | 60 | 52 |
设![]() 表示理财产品最满意度的百分比,
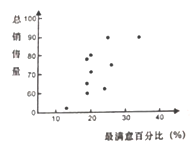
表示理财产品最满意度的百分比,![]() 为该理财产品的总销售量(万元).这些数据的散点图如图所示.
为该理财产品的总销售量(万元).这些数据的散点图如图所示.
(1)在![]() 份
份![]() 款型理财产品的顾客满意度调查资料中任取
款型理财产品的顾客满意度调查资料中任取![]() 份;只有一份最满意的,求含有最满意客户资料事件的概率.
份;只有一份最满意的,求含有最满意客户资料事件的概率.
(2)我们约定:相关系数的绝对值在![]() 以下是无线性相关,在
以下是无线性相关,在![]() 以上(含
以上(含![]() )至
)至![]() 是一般线性相关,在
是一般线性相关,在![]() 以上(含
以上(含![]() )是较强线性相关,若没有达到较强线性相关则采取“末位”剔除制度(即总销售量最少的那一款产品退出理财销售);试求在剔除“末位”款型后的线性回归方程(系数精确到
)是较强线性相关,若没有达到较强线性相关则采取“末位”剔除制度(即总销售量最少的那一款产品退出理财销售);试求在剔除“末位”款型后的线性回归方程(系数精确到![]() ).
).
数据参考计算值:
项目 |
|
|
|
|
|
|
值 | 21.9 | 72.1 | 288.9 | 37.16 | 452.1 | 17.00 |
附:回归直线方程![]() 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为:
线性相关系数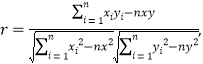
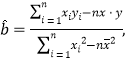
![]() .
.
