题目内容
【题目】以下5条表述中,横线上填A代表“充分非必要条件”,填B代表“必要非充分条件”,填C代表“充要条件”,填D代表“既非充分也非必要条件”,请将相应的字母填入下列横线上.
(1)若![]() ,则“
,则“![]() 是
是![]() 与
与![]() 的等比中项”是“
的等比中项”是“![]() ”的_______.
”的_______.
(2)“数列![]() 为常数列”是“数列
为常数列”是“数列![]() 既是等差数列又是等比数列”的_______.
既是等差数列又是等比数列”的_______.
(3)若![]() 是等比数列,则“
是等比数列,则“![]() ”是“
”是“![]() 为递减数列”的_______.
为递减数列”的_______.
(4)若![]() 是公比为
是公比为![]() 的等比数列,则“
的等比数列,则“![]() ”是“
”是“![]() 是递减数列”的_______.
是递减数列”的_______.
(5)记数列![]() 的前
的前![]() 项和为
项和为![]() ,则“数列
,则“数列![]() 为递增数列”是“数列
为递增数列”是“数列![]() 的各项均为大于零”的_______.
的各项均为大于零”的_______.
【答案】A B C D B
【解析】
根据充分条件、必要条件一一判断即可.
解:对于(1),![]() ,若
,若![]() 是
是![]() 与
与![]() 的等比中项则可得
的等比中项则可得![]() ,充分性成立,
,充分性成立,
若当![]() 时满足
时满足![]() 当时
当时![]() 不是
不是![]() 与
与![]() 的等比中项,故必要性不成立,即“
的等比中项,故必要性不成立,即“![]() 是
是![]() 与
与![]() 的等比中项”是“
的等比中项”是“![]() ”的充分不必要条件,故填
”的充分不必要条件,故填![]() ;
;
对于(2)若数列![]() 为常数列则数列
为常数列则数列![]() 是等差数列不一定是等比数列,如
是等差数列不一定是等比数列,如![]() 是各项均为
是各项均为![]() 的常数数列,故充分性不成立;
的常数数列,故充分性不成立;
若数列![]() 既是等差数列又是等比数列,则数列
既是等差数列又是等比数列,则数列![]() 一定为各项不为零的常数数列,故必要性成立;即“数列
一定为各项不为零的常数数列,故必要性成立;即“数列![]() 为常数列”是“数列
为常数列”是“数列![]() 既是等差数列又是等比数列”的必要不充分条件,故填
既是等差数列又是等比数列”的必要不充分条件,故填![]() ;
;
对于(3)已知数列![]() 是等比数,若
是等比数,若![]() 可得
可得![]() 为递减数列,故充分性成立;
为递减数列,故充分性成立;
若![]() 为递减数列,则必有
为递减数列,则必有![]() ,故必要性也成立,即“
,故必要性也成立,即“![]() ”是“
”是“![]() 为递减数列”的充要条件,故填
为递减数列”的充要条件,故填![]() ;
;
对于(4)![]() 是公比为
是公比为![]() 的等比数列,当
的等比数列,当![]() ,且
,且![]() 时,
时,![]() 是递减数列,或当
是递减数列,或当![]() ,且
,且![]() 时,
时,![]() 是递减数列,故“
是递减数列,故“![]() ”是“
”是“![]() 是递减数列”的既不充分也不必要条件,故填
是递减数列”的既不充分也不必要条件,故填![]() ;
;
对于(5)若数列![]() 为递增数列不能得到数列
为递增数列不能得到数列![]() 的各项均为大于零,故充分性不成立,若数列
的各项均为大于零,故充分性不成立,若数列![]() 的各项均为大于零则数列
的各项均为大于零则数列![]() 为递增数列,故必要性成立,即“数列
为递增数列,故必要性成立,即“数列![]() 为递增数列”是“数列
为递增数列”是“数列![]() 的各项均为大于零”的必要不充分条件,故填
的各项均为大于零”的必要不充分条件,故填![]() ;
;
故答案为:(1). A (2). B (3). C (4). D (5). B

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
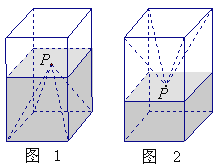
小学同步三练核心密卷系列答案【题目】如图1,一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有![]() 升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点
升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点![]() (图2).有下列四个命题:
(图2).有下列四个命题:
A.正四棱锥的高等于正四棱柱高的一半 |
B.将容器侧面水平放置时,水面也恰好过点 |
C.任意摆放该容器,当水面静止时,水面都恰好经过点 |
D.若往容器内再注入 |
其中真命题的代号是: (写出所有真命题的代号).