题目内容
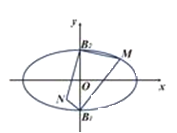
【题目】已知椭圆
为其左右焦点，
为其上下顶点，四边形
的面积为
.点
为椭圆
上任意一点，以为圆心的圆（记为圆）总经过坐标原点
.
（1）求椭圆的长轴
的最小值，并确定此时椭圆的方程；
（2）对于（1）中确定的椭圆，若给定圆
，则圆和圆
的公共弦
的长是否为定值？如果是，求
的值；如果不是，请说明理由.
【答案】（1）长轴
的最小值为
，此时椭圆
的方程为
；（2）2.
【解析】
（1）利用四边形
的面积求得
，利用基本不等式求得的最小值，同时求得椭圆的方程.（2）设出
点坐标，代入椭圆方程，得到点两个坐标的关系式.求得圆的方程和圆
的方程，两者作差求得公共弦所在直线方程，求得圆心到公共弦的距离，由此求得弦长
为定值.
解：（1）依题意四边形的面积为
因为长轴
当且仅当
时取“
”
此时
故长轴的最小值为，此时椭圆的方程为
（2）设点
为椭圆上任意一点，则
.
圆的方程为：
，
圆的方程为：
，
两式作差得公共弦方程为：
，
所以弦心距
则弦长
，所以圆和动圆的公共弦长为定值
.
鸿图图书寒假作业假期作业吉林大学出版社系列答案
【题目】郑汴一体化是依托郑州省会城市资源优势发展开封的省级战略，实施至今，取得了一系列的成就：两城电信同价，金融同城，郑开大道全线贯通，城际列车实常态化运营．随着郑汴一体化的深入推进，很多人认为郑州开封未来有望合并．为了解市民对郑汴合并的态度，现随机抽查55人，结果按年龄分类统计形成如下表格：
支持 | 反对 | 合计 | |
不足35岁 | 20 | ||
35岁以上 | 30 | ||
合计 | 25 | 55 |
（1）请完成上面的2×2列联表，并判断是否有99.5%的把握认为市民对郑汴合并的态度与年龄有关？
（2）在上述样木中用分层抽样的方法，从攴持郑汴合并的两组市民中随机抽取6人作进一步调查，从这6人中任选2人，求恰有1位“不足35岁”的市民和1位“35岁及以上”的市民的概率．
附：
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.814 | 5.024 | 7.879 | 10.828 |
