题目内容
【题目】若公差为
的无穷等差数列
的前
项和为
，则下列说法：（1）若
，则数列
有最大项；（2）若数列有最大项，则；（3）若数列是递增数列，则对任意
都有
；（4）若对任意都有，则数列是递增数列；其中正确的是______.（选序号）.
【答案】（1）（2）（4）
【解析】
由等差数列的求和公式可得
，可看作关于
的二次函数，由二次函数的性质逐一验证可得.
解：由等差数列的求和公式可得
对于（1）若
，由二次函数的性质可得数列
有最大项，故正确；
对于（2）若数列有最大项，则对应的抛物线开口向下，则有，故正确；
对于（3）若数列是递增数列，则对应的抛物线开口向上，但不一定有任意
均有
，故错误；
对于（4）若对任意都有，则对应的抛物线开口向上，
，可得数列是递增数列，故正确；
故答案为：（1）（2）（4）
【题目】在平面直角坐标系
中，①已知点
，
，
为曲线
上任一点，
到点
的距离和到点
的距离的比值为2；②圆经过
，
，且圆心在直线
上.从①②中任选一个条件.
（1）求曲线的方程；
（2）若直线
被曲线截得弦长为2，求
的值.
【题目】在2018年10月考考试中，成都外国语学校共有250名高三文科学生参加考试，数学成绩的频率分布直方图如图：
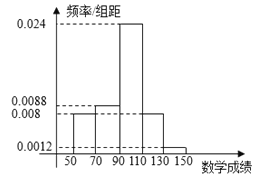
（1）如果成绩大于130的为特别优秀，这250名学生中本次考试数学成绩特别优秀的大约多少人？
（2）如果这次考试语文特别优秀的有5人，语文和数学两科都特别优秀的共有2人，从（1）中的数学成绩特别优秀的人中随机抽取2人，求选出的2人中恰有1名两科都特别优秀的概率．
（3）根据（1），（2）的数据，是否有99%以上的把握认为语文特别优秀的同学，数学也特别优秀？
①
②
P（ | 0.50 | 0.40 | … | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | … | 6.635 | 7.879 | 10.828 |
【题目】计划在某水库建一座至多安装3台发电机的水电站，过去50年的水文资料显示，水库年入流量
(年入流量：一年内上游来水与库区降水之和.单位：亿立方米）都在40以上.其中，不足80的年份有10年，不低于80且不超过120的年份有35年，超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率，并假设各年的年入流量相互独立.
（1）求未来4年中，至多1年的年入流量超过120的概率；
（2）水电站希望安装的发电机尽可能运行，但每年发电机最多可运行台数受年入流量
限制，并有如下关系:
年入流量 |
|
|
|
发电量最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行，则该台年利润为5000万元；若某台发电机未运行，则该台年亏损800万元，欲使水电站年总利润的均值达到最大，应安装发电机多少台？
【题目】某幼儿园举办“yue”主题系列活动——“悦”动越健康亲子运动打卡活动，为了解小朋友坚持打卡的情况，对该幼儿园所有小朋友进行了调查，调查结果如下表：
打卡天数 | 17 | 18 | 19 | 20 | 21 |
男生人数 | 3 | 5 | 3 | 7 | 2 |
女生人数 | 3 | 5 | 5 | 7 | 3 |
（1）根据上表数据，求该幼儿园男生平均打卡的天数；
（2）若从打卡21天的小朋友中任选2人交流心得，求选到男生和女生各1人的概率.
