8.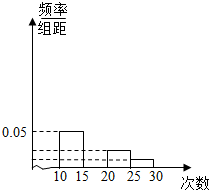 对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图:
对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图:
(1)求出表中M、p、m、n的值;
(2)补全频率分布直方图;若该校高一学生有360人,估计他们参加社区服务的次数在区间[15,20)内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间[20,25)内的概率.
 对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图:
对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图:| 分组 | 频数 | 频率 |
| [10,15) | 10 | 0.25 |
| [15,20) | 25 | n |
| [20,25) | m | p |
| [25,30) | 2 | 0.05 |
| 合计 | M | 1 |
(2)补全频率分布直方图;若该校高一学生有360人,估计他们参加社区服务的次数在区间[15,20)内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间[20,25)内的概率.
4.若函数f(x)为定义在R上的奇函数,且在(0,+∞)为减函数,若f(2)=0,则不等式(x-1)f(x-1)>0的解集为( )
| A. | (-3,-1) | B. | (-3,1)∪(2,+∞) | C. | (-3,0)∪(1,3) | D. | (-1,1)∪(1,3) |
3.已知函数$f(x)=\left\{\begin{array}{l}-{x^2}-ax-7,(x≤1)\\ \frac{a}{x}(x>1)\end{array}\right.$是R上的增函数,则a的取值范围是( )
| A. | -4≤a<0 | B. | a≤-2 | C. | -4≤a≤-2 | D. | a<0 |
2.若${log_a}\frac{4}{5}<1$,则实数a的取值范围是( )
| A. | $(0,\frac{4}{5})$ | B. | $(\frac{4}{5},+∞)$ | C. | $(\frac{4}{5},1)$ | D. | $(0,\frac{4}{5})$∪(1,+∞) |
20.设集合A={x|x2-x-2≤0},集合B={x|1<x≤3},则A∪B=( )
0 252006 252014 252020 252024 252030 252032 252036 252042 252044 252050 252056 252060 252062 252066 252072 252074 252080 252084 252086 252090 252092 252096 252098 252100 252101 252102 252104 252105 252106 252108 252110 252114 252116 252120 252122 252126 252132 252134 252140 252144 252146 252150 252156 252162 252164 252170 252174 252176 252182 252186 252192 252200 266669
| A. | {x|-1≤x≤3} | B. | {x|-1≤x<1} | C. | {x|1≤x≤2} | D. | {x|2<x≤3} |
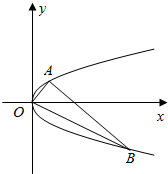 已知抛物线y2=2px(p>0)上点T(3,t)到焦点F的距离为4.
已知抛物线y2=2px(p>0)上点T(3,t)到焦点F的距离为4.