题目内容
8.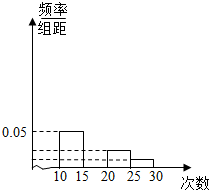 对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图:
对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图:| 分组 | 频数 | 频率 |
| [10,15) | 10 | 0.25 |
| [15,20) | 25 | n |
| [20,25) | m | p |
| [25,30) | 2 | 0.05 |
| 合计 | M | 1 |
(2)补全频率分布直方图;若该校高一学生有360人,估计他们参加社区服务的次数在区间[15,20)内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间[20,25)内的概率.
分析 (1)根据$\frac{频数}{数据总数}$=频率及频率之和等于1,频数之和等于数据总数,列出方程可求出;
(2)根据频率分布直方图的高度=$\frac{频率}{组距}$可求出[15,20)组的直方图高度,作出图象即可,用高一总人数乘该组的频率即可得到高一学生服务次数在[15,20)内的总人数;
(3)使用列举法求出概率.
解答 解:(1)由题可知$\frac{10}{M}=0.25$,$\frac{25}{M}=n$,$\frac{m}{M}=p$,.
又 10+25+m+2=M,解得 M=40,n=0.625,m=3,p=0.075.
(2)由(1)可知,[15,20)组的频率与组距之比为0.125.则频率分布直方图如下:
参加在社区服务次数在区间[15,20)内的人数为360×0.625=225人.
(3)在样本中,处于[20,25)内的人数为3,可分别记为A,B,C,处于[25,30)内的人数为2,可分别记为a,b.从该5名同学中取出2人的取法有(A,a),(A,b),(B,a)(B,b),(C,a),(C,b),(A,B),(A,C),(B,C),(a,b)共10种,且他们出现的机会均等;至多一人参加社区服务次数在区间[20,25)内的情况有(A,a),(A,b),(B,a),(B,b),(C,a),(C,b),(a,b)共7种,所以至多一人参加社区服务次数在区间[20,25)内的概率为$\frac{7}{10}$.
点评 本题考查了频率分布直方图及古典概型的概率公式,是基础题.

练习册系列答案
相关题目
14.若f(x+π)=f(x),且f(-x)=f(x),则f(x)可以是( )
| A. | sin2x | B. | cosx | C. | cos|x| | D. | |sinx| |
3.已知函数$f(x)=\left\{\begin{array}{l}-{x^2}-ax-7,(x≤1)\\ \frac{a}{x}(x>1)\end{array}\right.$是R上的增函数,则a的取值范围是( )
| A. | -4≤a<0 | B. | a≤-2 | C. | -4≤a≤-2 | D. | a<0 |
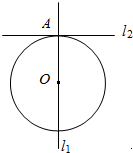 如图,已知l1⊥l2,圆心在l1上,半径为1m的圆O在t=0时与l2相切于点A,圆O沿l1以1m/s的速度匀速向上移动,圆被直线l2所截上方圆弧长记为x,令y=$si{n^2}\frac{x}{2}$,则y与时间t(0≤t≤1,单位:s)的函数y=f(t)的图象大致为( )
如图,已知l1⊥l2,圆心在l1上,半径为1m的圆O在t=0时与l2相切于点A,圆O沿l1以1m/s的速度匀速向上移动,圆被直线l2所截上方圆弧长记为x,令y=$si{n^2}\frac{x}{2}$,则y与时间t(0≤t≤1,单位:s)的函数y=f(t)的图象大致为( )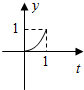

 已知函数f(x)=x2+2x|x-a|,其中a∈R.
已知函数f(x)=x2+2x|x-a|,其中a∈R.