19.偶函数y=f(x)满足下列条件①x≥0时,f(x)=x3;②对任意x∈[t,t+1],不等式f(x+t)≥8f(x)恒成立,则实数t的取值范围是( )
| A. | (-∞,-$\frac{3}{4}$] | B. | [-$\frac{3}{4},0$] | C. | [-2,$\frac{3}{4}$] | D. | [-$\frac{4}{3},1$] |
18.已知f(x)=$\left\{\begin{array}{l}{-{x}^{2},x≥0}\\{{x}^{2}+2x,x<0}\end{array}\right.$,则f(f(x))≤3的解集为( )
| A. | (-∞,-3] | B. | [-3,+∞) | C. | (-∞,$\sqrt{3}$] | D. | [$\sqrt{3}$,+∞) |
17.实系数一元二次方程x2+ax+2b=0的一个根在(0,1)上,另一个根在(1,2)上,则$\frac{b-3}{a-1}$的取值范围是( )
| A. | [1,3] | B. | (1,3) | C. | $[{\frac{1}{2},\frac{3}{2}}]$ | D. | $({\frac{1}{2},\frac{3}{2}})$ |
16.数列{an}满足${a_n}-{({-1})^n}{a_{n-1}}=n,({n≥2})$,Sn是{an}的前n项和,则S40=( )
| A. | 880 | B. | 900 | C. | 440 | D. | 450 |
15.函数f(x)=$\left\{\begin{array}{l}a{x^2}+x-1(x>2)\\ ax-1(x≤2)\end{array}$是R上的单调递减函数,则实数a的取值范围是( )
| A. | -$\frac{1}{4}$≤a<0 | B. | a≤-$\frac{1}{4}$ | C. | -1≤a≤-$\frac{1}{4}$ | D. | a≤-1 |
11.由直线x=1,x=2,y=0与曲线y=$\frac{1}{x}$所围成的曲边梯形,将区间[1,2]等分成4份,将曲边梯形较长的边近似看作高,则曲边梯形的面积是( )
0 251825 251833 251839 251843 251849 251851 251855 251861 251863 251869 251875 251879 251881 251885 251891 251893 251899 251903 251905 251909 251911 251915 251917 251919 251920 251921 251923 251924 251925 251927 251929 251933 251935 251939 251941 251945 251951 251953 251959 251963 251965 251969 251975 251981 251983 251989 251993 251995 252001 252005 252011 252019 266669
| A. | $\frac{9}{20}$ | B. | $\frac{37}{60}$ | C. | $\frac{319}{420}$ | D. | $\frac{259}{420}$ |
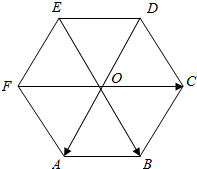 如图所示.O是正六边形ABCDEF的中心,且$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,$\overrightarrow{OC}=\overrightarrow{c}$.
如图所示.O是正六边形ABCDEF的中心,且$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,$\overrightarrow{OC}=\overrightarrow{c}$.