6.已知函数f(x)=$\frac{2{x}^{2}}{x+1}$,函数g(x)=asin($\frac{π}{6}$x)-2a+2(a>0),若存在x1∈[0,1],对任意x2∈[0,1]都有f(x1)=g(x2)成立,则实数a的取值范围是( )
| A. | ($\frac{1}{2}$,1] | B. | [$\frac{2}{3}$,1) | C. | [$\frac{2}{3}$,1] | D. | [$\frac{2}{3}$,2] |
5.若四边形ABCD满足:$\overrightarrow{AB}$+$\overrightarrow{CD}$=0,($\overrightarrow{AB}$+$\overrightarrow{DA}$)•$\overrightarrow{AC}$=0,则该四边形一定是( )
| A. | 矩形 | B. | 正方形 | C. | 菱形 | D. | 直角梯形 |
4.设集合M={x|2x2-x-6<0},N={x|0<x≤4},则M∩N等于( )
| A. | (0,2) | B. | (-$\frac{3}{2}$,0) | C. | (-2,3) | D. | (-2,2) |
20.设实数x,y满足:$\left\{\begin{array}{l}{2x+y≤4}\\{x-2y≤2}\\{x-y≥1}\end{array}\right.$,O为坐标原点,则x2+y2的最小值是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
18.若集合M={x|x2+x-2≤0},N={-2,-1,1,2},则M∩N等于( )
0 250253 250261 250267 250271 250277 250279 250283 250289 250291 250297 250303 250307 250309 250313 250319 250321 250327 250331 250333 250337 250339 250343 250345 250347 250348 250349 250351 250352 250353 250355 250357 250361 250363 250367 250369 250373 250379 250381 250387 250391 250393 250397 250403 250409 250411 250417 250421 250423 250429 250433 250439 250447 266669
| A. | {-1,1,2} | B. | {1} | C. | {-1,1} | D. | {-2,-1,1} |
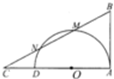 如图,已知AD为半圆O的直径,AB为半圆O的切线,割线BMN交AD的延长线于点C,且BM=MN=NC,AB=2$\sqrt{2}$.
如图,已知AD为半圆O的直径,AB为半圆O的切线,割线BMN交AD的延长线于点C,且BM=MN=NC,AB=2$\sqrt{2}$.