题目内容
17.设等比数列{an}的公比q=$\frac{1}{2}$,前n项和为Sn,则$\frac{{S}_{3}}{{a}_{3}}$=( )| A. | 5 | B. | 7 | C. | 8 | D. | 15 |
分析 利用等比数列的通项公式与前n项和公式即可得出.
解答 解:S3=$\frac{{a}_{1}(1-\frac{1}{{2}^{3}})}{1-\frac{1}{2}}$=$\frac{7}{4}{a}_{1}$,a3=${a}_{1}(\frac{1}{2})^{2}$=$\frac{1}{4}{a}_{1}$,
∴$\frac{{S}_{3}}{{a}_{3}}$=7.
故选:B.
点评 本题考查了等比数列的通项公式与前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
7.实验人员获取一组数据如表:则拟合效果最接近的一个为( )
| x | 1.99 | 3 | 4 | 5.1 | 6.12 |
| y | 1.5 | 4.04 | 7.5 | 12 | 18.01 |
| A. | y=2x-2 | B. | y=$\frac{1}{2}$(x2-1) | C. | y=log2x | D. | y=${(\frac{1}{2})^x}$ |
9.某种鲜花进价每束2.5元,售价每束5元,若卖不出,则以每束1.6元的价格处理掉,某节日鲜花的需求量X(单位:束)的分布列为
(Ⅰ)若进鲜花400束,是写出销售量S(单位:束)的分布列,并求利润Y的均值.
(Ⅱ)若进鲜花n束(300<n≤500),求n取何值时可使利润Y的均值最大?
| X | 200 | 300 | 400 | 500 |
| P | 0.20 | 0.35 | 0.30 | 0.15 |
(Ⅱ)若进鲜花n束(300<n≤500),求n取何值时可使利润Y的均值最大?
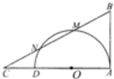 如图,已知AD为半圆O的直径,AB为半圆O的切线,割线BMN交AD的延长线于点C,且BM=MN=NC,AB=2$\sqrt{2}$.
如图,已知AD为半圆O的直径,AB为半圆O的切线,割线BMN交AD的延长线于点C,且BM=MN=NC,AB=2$\sqrt{2}$.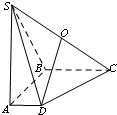 如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AB⊥AD,AB⊥BC,侧棱SA⊥底面ABCD,点O为侧棱SC的中点,且SA=AB=BC=2,AD=1.
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AB⊥AD,AB⊥BC,侧棱SA⊥底面ABCD,点O为侧棱SC的中点,且SA=AB=BC=2,AD=1.