10.已知非零向量$\overrightarrow{OA}$=(a,0),$\overrightarrow{OB}$=(0,a),$\overrightarrow{OC}$=(1,2),若A,B,C三点共线,则a=( )
| A. | -1 | B. | 1 | C. | 3 | D. | 0或3 |
9.若在区间[-1,2]中随机地取一个数k,则使函数在f(x)=kx+1在R上为增函数的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
8.已知cosα=-$\frac{3}{5}$,且α∈(-π,0),则tanα=( )
| A. | -$\frac{4}{3}$ | B. | $\frac{4}{3}$ | C. | -$\frac{3}{4}$ | D. | $\frac{3}{4}$ |
6.在中学综合素质评价某个维度的测评中,分“优秀、合格、尚待改进”三个等级进行学生互评,某校高二年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高二年级抽取了45名学生的测评结果,并作出频数统计表如下:
表1:男生
表2:女生
(1)从表2的非优秀学生中随机选取2人交谈,求所选2人中恰有1人测评等级为合格的概率;
(2)由表中统计数据填写下边2×2列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
参考数据与公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$临界值表
表1:男生
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | x | 5 |
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | 3 | y |
(2)由表中统计数据填写下边2×2列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
| 男生 | 女生 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
3.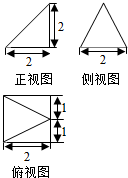 已知某几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体得体积是( )cm2.
已知某几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体得体积是( )cm2.
 已知某几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体得体积是( )cm2.
已知某几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体得体积是( )cm2.| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 2 | D. | 4 |
2.复数z=-4i+3的虚部是( )
0 247782 247790 247796 247800 247806 247808 247812 247818 247820 247826 247832 247836 247838 247842 247848 247850 247856 247860 247862 247866 247868 247872 247874 247876 247877 247878 247880 247881 247882 247884 247886 247890 247892 247896 247898 247902 247908 247910 247916 247920 247922 247926 247932 247938 247940 247946 247950 247952 247958 247962 247968 247976 266669
| A. | -4i | B. | 3i | C. | 3 | D. | -4 |