题目内容
9.若在区间[-1,2]中随机地取一个数k,则使函数在f(x)=kx+1在R上为增函数的概率是( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
分析 由题意,本题是几何概型,只要求出k对应事件的长度为区间长度,求出使函数在f(x)=kx+1在R上为增函数的k的范围,利用公式解答.
解答 解:由题意,本题是几何概型,k满足的区间[-1,2]长度为3,而在此条件下满足使函数在f(x)=kx+1在R上为增函数的x的范围是(0,2],区间长度为2,
由几何概型的概率公式得到在区间[-1,2]中随机地取一个数k,则使函数在f(x)=kx+1在R上为增函数的概率是$\frac{2}{3}$;
故选A.
点评 本题考查了几何概型的概率求法;关键是明确概率模型,选择正确的事件测度,利用长度、面积或者体积比求概率.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
20.在△ABC中,角A为钝角,AB=1,AC=3,AD为BC边上的高,已知$\overrightarrow{AD}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则x的取值范围为( )
| A. | ($\frac{3}{4}$,$\frac{9}{10}$) | B. | ($\frac{1}{2}$,$\frac{9}{10}$) | C. | ($\frac{3}{5}$,$\frac{3}{4}$) | D. | ($\frac{1}{2}$,$\frac{3}{4}$) |
14.已知锐角α终边经过点P(cos50°,1+sin50°).则锐角α等于( )
| A. | 10° | B. | 20° | C. | 70° | D. | 80° |
1.已知f′(x)是函数f(x)的导数,f(x)=f′(1)•2x+x2,f′(2)=( )
| A. | $\frac{12-8ln2}{1-2ln2}$ | B. | $\frac{2}{1-2ln2}$ | C. | $\frac{4}{1-2ln2}$ | D. | -2 |
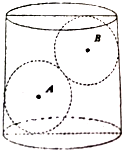 如图,在水平放置的直径与高相等的圆柱内,放入两个半径相等的小球(球A和球B),圆柱的底面直径为2+$\sqrt{2}$,向圆柱内注满水,水面刚好淹没小球B
如图,在水平放置的直径与高相等的圆柱内,放入两个半径相等的小球(球A和球B),圆柱的底面直径为2+$\sqrt{2}$,向圆柱内注满水,水面刚好淹没小球B