2.下列说法错误的是( )
| A. | 设有一个回归方程为$\widehat{y}$=3-5x,则变量x每增加一个单位,y平均增加5个单位 | |
| B. | 回归直线$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$必过点($\overline{x}$,$\overline{y}$) | |
| C. | 在一个2×2列联表中,由计算得随机变量K2的观测值k=13.079,则可以在犯错误的概率不超过0.001的前提下,认为这两个变量间有关系 | |
| D. | 将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变 |
20.观察下列各式:

照此规律,当n∈N*时,C2n-10+C2n-11+C2n-12+…+C2n-1n-1=( )

照此规律,当n∈N*时,C2n-10+C2n-11+C2n-12+…+C2n-1n-1=( )
| A. | 4n+1 | B. | 4n | C. | 4n-1 | D. | 4n-2 |
19.在极坐标系中,直线ρcosθ=1与圆ρ=2cosθ的位置关系是( )
| A. | 相离 | B. | 相切 | C. | 相交但不过圆心 | D. | 相交且过圆心 |
18.如图1是一个边长为1的正三角形,分别连接这个三角形三边中点,将在三角剖分成4个三角开(如图2),再分别连接图2中一个小三角形三边的中点,又可将原三角形剖分成7个三角形(如图3),…,依此类推,设第n个图中原三角形被剖分成an个三角形,则第4个图中最小三角形的边长为( );a100=( )
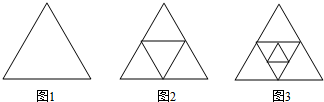

| A. | $\frac{1}{6}$,300 | B. | $\frac{1}{8}$,300 | C. | $\frac{1}{6}$,298 | D. | $\frac{1}{8}$,298 |
15.已知数列{an}、{bn}、{cn}的通项公式分别为:an=n,bn=n(n+1),cn=n(n+1)(n+2),数列{an},{bn}的前n项和分别为S1(n),S2(n),观察下表:
发现S1(n)=$\frac{1}{2}$bn,并可用下面方法证明:
因为ak=k=$\frac{1}{2}[k(k+1)-(k-1)k]$,k=1,2,…n,
所以S1(n)=a1+a2+…an=1+2+…+n=$\frac{1}{2}{(1×2-0×1)+(2×3-1×2)…+[n(n+1)-(n-1)n]}$=$\frac{1}{2}n(n+1)=\frac{1}{2}{b}_{n}$.
(1)指出S2(n)与cn的关系,并类比上面方法证明你的结论;
(2)求和Tn=12+22+…+n2.
0 247569 247577 247583 247587 247593 247595 247599 247605 247607 247613 247619 247623 247625 247629 247635 247637 247643 247647 247649 247653 247655 247659 247661 247663 247664 247665 247667 247668 247669 247671 247673 247677 247679 247683 247685 247689 247695 247697 247703 247707 247709 247713 247719 247725 247727 247733 247737 247739 247745 247749 247755 247763 266669
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | … |
| an | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | … |
| S1(n) | 1 | 3 | 6 | 10 | 15 | 21 | 28 | 36 | … |
| bn | 2 | 6 | 12 | 20 | 30 | 42 | 56 | 72 | … |
因为ak=k=$\frac{1}{2}[k(k+1)-(k-1)k]$,k=1,2,…n,
所以S1(n)=a1+a2+…an=1+2+…+n=$\frac{1}{2}{(1×2-0×1)+(2×3-1×2)…+[n(n+1)-(n-1)n]}$=$\frac{1}{2}n(n+1)=\frac{1}{2}{b}_{n}$.
(1)指出S2(n)与cn的关系,并类比上面方法证明你的结论;
(2)求和Tn=12+22+…+n2.