题目内容

19．在极坐标系中，直线ρcosθ=1与圆ρ=2cosθ的位置关系是（　　）
A．相离B．相切C．相交但不过圆心D．相交且过圆心

分析 利用$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$即可化为直角坐标方程，进而判断出位置关系．

解答 解：直线ρcosθ=1即x=1．
圆ρ=2cosθ即ρ2=2ρcosθ，化为x2+y2=2x，配方为（x-1）2+y2=1．其圆心为（1，0）．
可知：直线x=1经过圆心（1，0）．
∴直线ρcosθ=1与圆ρ=2cosθ的位置关系是相交且过圆心．
故选：D．

点评 本题考查了极坐标化为直角坐标方程、直线与圆的位置关系，考查了计算能力，属于基础题．

练习册系列答案
相关题目
9．已知圆C1：x2+y2+2x+2y-8=0与圆C2：x2+y2-2x+10y-24=0相交于AB两点，则公共弦AB所在直线方程为x-2y+4=0．
10．已知空间两条不同的直线m，n和两个不同的平面α，β，则下列命题正确的是④
①若m∥α，n?α，则m∥n；  ②若α∩β=m，m⊥n，则n⊥α
③若m∥α，n∥α，则m∥n；  ④若m∥α，m?β，α∩β=n，则m∥n．
7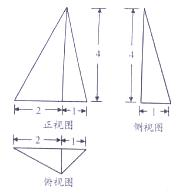．若某几何体的三视图如图所示，则该几何体的体积为（　　）
A．1B．$\frac{4}{3}$C．2D．6
14．设函数f（x）=x2+aln（x+1）．
（1）若a=-12，写出函数f（x）的单调区间；
（2）若函数f（x）在[2，+∞）上单调递增，求实数a的取值范围；
（3）若在区间[0，1]上，函数f（x）在x=0处取得最大值，求实数a的取值范围．
4．已知函数f（x）=$\frac{ln（x-2m）}{x}$，m为实数．
（1）若m=-$\frac{1}{2}$，证明：函数f（x）是（0，+∞）上的减函数；
（2）若m＜$\frac{1}{2}$，曲线y=f（x）在点（1，f（1））处的切线与直线x-y=0平行，求m的值；
（3）若x＞0，证明：$\frac{{ln（{x+1}）}}{x}＞\frac{x}{{{e^x}-1}}$（其中e=2.71828…是自然对数的底数）．
7．为了创建全国卫生城市，在湛江市民中选8名青年志愿者，其中有3名男青年志愿者，5名女青年志愿者，现从中选3人参加“创建全国卫生城市”户外活动导引工作，则这3人中既有男青年志愿者又有女青年志愿者的概率为（　　）
A．$\frac{45}{512}$B．$\frac{75}{512}$C．$\frac{15}{64}$D．$\frac{45}{56}$
4．已知顶点在原点O，准线方程是y=-1的抛物线与过点M（0，1）的直线l交于A，B两点，若直线OA和直线OB的斜率之和为1
（Ⅰ）求此抛物线的标准方程；
（Ⅱ）求直线l的方程．
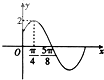5．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示．
（1）求函数f（x）的解析式；
（2）求方程f（$\frac{3x}{4}$-$\frac{π}{8}$）=f（$\frac{π}{2}$）的解．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网