题目内容
1.已知函数f(x)=ex-alnx的定义域是(0,+∞),关于函数f(x)给出下列命题:①对于任意a∈(0,+∞),函数f(x)存在最小值;
②对于任意a∈(-∞,0),函数f(x)是(0,+∞)上的减函数;
③存在a∈(-∞,0),使得对于任意的x∈(0,+∞),都有f(x)>0成立;
④存在a∈(0,+∞),使得函数f(x)有两个零点.
其中正确命题的序号是①④.
分析 先求导数,若为减函数则导数恒小于零;在开区间上,若有最小值则有唯一的极小值,若有零点则对应方程有根.
解答 解:由对数函数知:函数的定义域为:(0,+∞),f′(x)=ex-$\frac{a}{x}$,
①∵a∈(0,+∞),∴存在x有f′(x)=ex-$\frac{a}{x}$=0,可以判断函数有最小值,①正确,
②∵a∈(-∞,0)∴f′(x)=ex-$\frac{a}{x}$≥0,是增函数.所以②错误,
③画出函数y=ex,y=-alnx的图象,如图:显然不正确.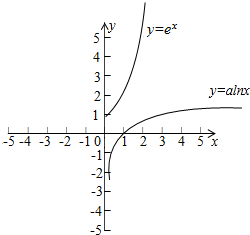
④令函数y=ex是增函数,y=alnx是减函数,所以存在a∈(0,+∞),f(x)=ex-alnx=0有两个根,正确.
故答案为:①④.
点评 本题主要考查导数法研究函数的单调性、极值、最值等问题.

练习册系列答案
相关题目
12.对函数f(x),在使f(x)≥M成立的所有常数M中,我们把M的最大值叫做函数f(x)的下确界.现已知定义在R上的偶函数f(x)满足f(1-x)=f(1+x),当x∈[0,1]时,f(x)=-3x2+2,则f(x)的下确界为( )
| A. | 2 | B. | 1 | C. | 0 | D. | -1 |
9.12名同学分别到三个企业进行社会调查,若每个企业4人,则不同的分配方案共有( )种.
| A. | $C_{12}^4C_8^4C_4^4$ | B. | $3C_{12}^4C_8^4C_4^4$ | ||
| C. | $C_{12}^4C_8^4A_3^3$ | D. | $\frac{{C_{12}^4C_8^4C_4^4}}{A_3^3}$ |