3.已知F1,F2分别是双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{5}$=1的左、右焦点,A是双曲线左支上异于顶点的一动点,圆C为△AF1F2的内切圆,若M(x,0)是其中的一个切点,则( )
| A. | x>-3 | B. | x<-3 | ||
| C. | x=-3 | D. | x与-3的大小不确定 |
2.已知f(x+1)=x-1+ex+1,则函数f(x)在点(0,f(0))处的切线与坐标轴围成的三角形的面积为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
1.曲线C的方程为$\sqrt{(x-1)^{2}+{y}^{2}}$+$\sqrt{(x+1)^{2}+{y}^{2}}$=2,若直线l:y=kx+1-2k的曲线C有公共点,则k的取值范围是( )
| A. | [$\frac{1}{3}$,1] | B. | ($\frac{1}{3}$,1) | C. | (-∞,$\frac{1}{3}$]∪[1,+∞) | D. | (-∞,$\frac{1}{3}$)∪(1,+∞) |
20.某程序框图如图所示,则输出的结果为( )
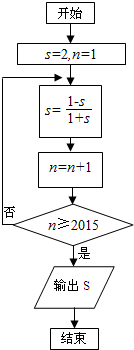

| A. | $\frac{1}{2}$ | B. | 2 | C. | -$\frac{1}{3}$ | D. | -3 |
19.设f′(x)是f(x)的导函数,f″(x)是f′(x)的导函数,若函数f(x)在区间I上恒有f″(x)≥0,则称f(x)是区间I上的凸函数,则下列函数在[-1,1]上是凸函数的是( )
| A. | f(x)=sinx | B. | f(x)=-cosx | C. | f(x)=x3-x | D. | f(x)=-ex |
18.设点P(x,y),则“x=2且y=-1”是“点P在圆(x-2)2+y2=1上”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
17.命题“?x0>0,2x0<x02”的否定为( )
| A. | ?x>0,2x<x2 | B. | ?x>0,2x≥x2 | C. | ?x≤0,2x<x2 | D. | ?x≤0,2x≥x2 |
16.若复数z满足iz=1+i,则z的虚部为( )
0 247093 247101 247107 247111 247117 247119 247123 247129 247131 247137 247143 247147 247149 247153 247159 247161 247167 247171 247173 247177 247179 247183 247185 247187 247188 247189 247191 247192 247193 247195 247197 247201 247203 247207 247209 247213 247219 247221 247227 247231 247233 247237 247243 247249 247251 247257 247261 247263 247269 247273 247279 247287 266669
| A. | 1 | B. | i | C. | -1 | D. | -i |