2. 某电影院统计电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述电影放映场次逐年变化规律的是( )
某电影院统计电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述电影放映场次逐年变化规律的是( )
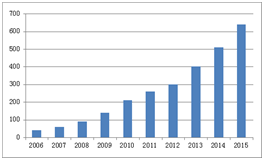
 某电影院统计电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述电影放映场次逐年变化规律的是( )
某电影院统计电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述电影放映场次逐年变化规律的是( )| A. | y=ax2+bx+c | B. | y=aex+b | C. | y=ax3+b | D. | y=alnx+b |
19.若函数y=f(x)满足,存在x0≠0,x0≠$\frac{1}{x_0}$,使$f({x_0})=f(\frac{1}{x_0})=0$,则x0叫做函数y=f(x)的“基点”,已知函数f(x)=x3+ax2+bx+1存在“基点”,则a2+(b-2)2的取值范围是( )
| A. | [2,+∞) | B. | [4,+∞) | C. | [8,+∞) | D. | [10,+∞) |
18.在△ABC中,E为AC上一点,且$\overrightarrow{AC}=4\overrightarrow{AE}$,P为BE上一点,且$\overrightarrow{AP}=m\overrightarrow{AB}+n\overrightarrow{AC}$(m>0,n>0),则$\frac{1}{m}+\frac{1}{n}$取最小值时,向量$\overrightarrow{a}$=(m,n)的模为( )
| A. | $\frac{{\sqrt{5}}}{4}$ | B. | $\frac{{\sqrt{6}}}{6}$ | C. | $\frac{{\sqrt{5}}}{6}$ | D. | 2 |
16.若框图所给的程序运行结果为S=90.那么判断框中应填入后的条件是( )
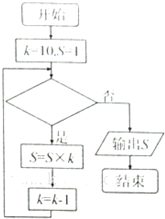

| A. | k=9 | B. | k≤8 | C. | k<8 | D. | k>8 |
15.已知集合A={x|x2-2x-3<0},Z为整数集,则集合A∩Z中所有元素的和为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
14.某企业有甲、乙两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在[29.94,30.06)的零件为优质品.
从甲、乙两个分厂生产的零件中各抽出500件,量其内径尺寸的结果如下表:
甲厂的零件内径尺寸:
乙厂的零件内径尺寸:
(Ⅰ)由以上统计数据填下面2×2列联表,并问是否有99.9%的把握认为“生产的零件是否为优质品与在不同分厂生产有关”;
附:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$
(Ⅱ)现用分层抽样方法(按优质品和非优质品分两层)从乙厂中抽取5件零件,求从这5件零件中任意取出2件,至少有1件非优质品的概率.
0 246944 246952 246958 246962 246968 246970 246974 246980 246982 246988 246994 246998 247000 247004 247010 247012 247018 247022 247024 247028 247030 247034 247036 247038 247039 247040 247042 247043 247044 247046 247048 247052 247054 247058 247060 247064 247070 247072 247078 247082 247084 247088 247094 247100 247102 247108 247112 247114 247120 247124 247130 247138 266669
从甲、乙两个分厂生产的零件中各抽出500件,量其内径尺寸的结果如下表:
甲厂的零件内径尺寸:
| 分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
| 频数 | 15 | 30 | 125 | 198 | 77 | 35 | 20 |
| 分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) | ||||
| 频数 | 40 | 70 | 79 | 162 | 59 | 55 | 35 | ||||
| 甲厂 | 乙厂 | 合计 | |
| 优质品 | |||
| 非优质品 | |||
| 合计 |
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.025 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
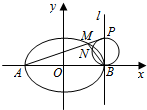 已知A、B分别为曲线C:$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>0)与x轴的左、右两个交点,直线l过点B且与x轴垂直,P为l上异于点B的点,连结AP与曲线C交于点M.
已知A、B分别为曲线C:$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>0)与x轴的左、右两个交点,直线l过点B且与x轴垂直,P为l上异于点B的点,连结AP与曲线C交于点M.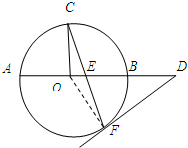 如图,AB是⊙O的直径,C,F是⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D.连结CF交AB于点E,OA=3,DB=3,则DE=3$\sqrt{3}$.
如图,AB是⊙O的直径,C,F是⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D.连结CF交AB于点E,OA=3,DB=3,则DE=3$\sqrt{3}$.