11.某班主任对全班50名学生学习积极性和参加社团活动情况进行调查,统计数据表1
(1)如果随机从该班抽查一名学生,抽到参加社团活动的学生的概率是多少?抽到不参加社团活动且学习积极性一般的学生的概率是多少?
(2)运用独立检验的思想方法分析:学生的学习积极性与参加社团活动情况是否有关系?并说明理由.
${Χ^2}=\frac{{n{{({{n_{11}}{n_{22}}-{n_{12}}{n_{21}}})}^2}}}{{{n_{1+}}{n_{2+}}{n_{+1}}{n_{+2}}}}$
(1)抽到参加社团活动的学生的概率是$\frac{11}{25}$,抽到不参加社团活动且学习积极性一般的学生的概率是$\frac{2}{5}$;
(2)有99.9%的把握认为学生的学习积极性与参加社团活动的态度有关系.
| 参加社团活动 | 不参加社团活动 | 合计 | |
| 学习积极性高 | 17 | 8 | 25 |
| 学习积极性一般 | 5 | 20 | 25 |
| 合计 | 22 | 28 | 50 |
(2)运用独立检验的思想方法分析:学生的学习积极性与参加社团活动情况是否有关系?并说明理由.
| P(Χ2≥k) | 0.05 | 0.01 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
(1)抽到参加社团活动的学生的概率是$\frac{11}{25}$,抽到不参加社团活动且学习积极性一般的学生的概率是$\frac{2}{5}$;
(2)有99.9%的把握认为学生的学习积极性与参加社团活动的态度有关系.
10.已知集合$A=\left\{{\left.x\right|{2^{{x^2}-x-2}}≤1}\right\}$,B={x|y=ln(1-x)},则A∩∁RB=( )
0 246875 246883 246889 246893 246899 246901 246905 246911 246913 246919 246925 246929 246931 246935 246941 246943 246949 246953 246955 246959 246961 246965 246967 246969 246970 246971 246973 246974 246975 246977 246979 246983 246985 246989 246991 246995 247001 247003 247009 247013 247015 247019 247025 247031 247033 247039 247043 247045 247051 247055 247061 247069 266669
| A. | (1,2) | B. | [1,2] | C. | [-1,1) | D. | (-1,1) |
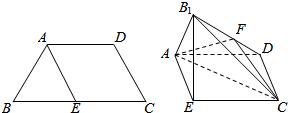 已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿AE折起到△B1AE的位置,使平面B1AE⊥平面AECD,F为B1D的中点.
已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿AE折起到△B1AE的位置,使平面B1AE⊥平面AECD,F为B1D的中点.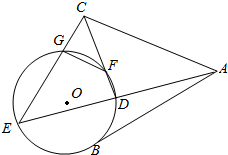 如图,AB是圆O的一条切线,切点为B,ADE,CFD,CGE都是圆O的割线,已知AC=AB.
如图,AB是圆O的一条切线,切点为B,ADE,CFD,CGE都是圆O的割线,已知AC=AB.