19.已知三棱锥S-ABC的所有顶点都在球O的表面上,△ABC是边长为1的正三角形,SC为球O的直径,且SC=2,则此三棱锥的体积为( )
| A. | $\frac{1}{4}$ | B. | $\frac{{\sqrt{2}}}{4}$ | C. | $\frac{{\sqrt{2}}}{6}$ | D. | $\frac{{\sqrt{2}}}{12}$ |
18.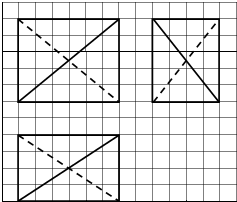 如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某多面件的三视图,该多面体的体积为( )
如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某多面件的三视图,该多面体的体积为( )
 如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某多面件的三视图,该多面体的体积为( )
如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某多面件的三视图,该多面体的体积为( )| A. | 40cm3 | B. | 50cm3 | C. | 60cm3 | D. | 80cm3 |
17.过椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$的右焦点F作两条相互垂直的直线分别交椭圆于A,B,C,D四点,则$\frac{1}{|AB|}+\frac{1}{|CD|}$的值为( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{6}$ | C. | 1 | D. | $\frac{7}{12}$ |
16.设集合M={x|2x2-y2=1},N={y|y=x2},则M∩N=( )
| A. | {(1,1)} | B. | {(-1,1),(1,1)} | C. | $[{\frac{1}{2},+∞})$ | D. | $[{\frac{{\sqrt{2}}}{2},+∞})$ |
11.设f(x)=cos2x-$\sqrt{3}$sin2x,把y=f(x)的图象向左平移φ(φ>0)个单位后,恰好得到函数g(x)=-cos2x-$\sqrt{3}$sin2x的图象,则φ的值可以为( )
0 246859 246867 246873 246877 246883 246885 246889 246895 246897 246903 246909 246913 246915 246919 246925 246927 246933 246937 246939 246943 246945 246949 246951 246953 246954 246955 246957 246958 246959 246961 246963 246967 246969 246973 246975 246979 246985 246987 246993 246997 246999 247003 247009 247015 247017 247023 247027 247029 247035 247039 247045 247053 266669
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
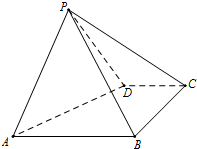 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD是以AD为底的等腰三角形.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD是以AD为底的等腰三角形.