10.如图,有一个几何体的三视图及其尺寸(单位:cm),则该几何体的表面积和体积分别为( )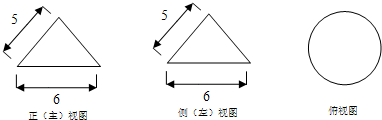

| A. | 24πcm2,12πcm3 | B. | 15πcm2,12πcm3 | C. | 24πcm2,36πcm3 | D. | 15πcm2,36πcm3 |
8.直线x=0的斜率为( )
| A. | 0 | B. | $\frac{π}{2}$ | C. | 1 | D. | 不存在 |
7.定义:$\frac{n}{{p}_{1}+{p}_{1}+…+{p}_{n}}$为n个p1,p2,…pn的“均倒数”,若已知正数数列{an}的前n项的”均倒数“为$\frac{1}{2n+1}$,又bn=$\frac{{a}_{n}-1}{2}$.,$\frac{1}{{b}_{1}{b}_{2}}$+$\frac{1}{{b}_{2}{b}_{3}}$+…+$\frac{1}{{b}_{2014}{b}_{2015}}$=( )
| A. | $\frac{2013}{4027}$ | B. | $\frac{4026}{4027}$ | C. | $\frac{2014}{4029}$ | D. | $\frac{4028}{4029}$ |
5.某超市从2014年甲、乙两种酸奶的日销售量(单位:箱)的数据中分別随机抽取100个.整理得到数据分组及频率分布表和频率分布直方图:

(Ⅰ)写出频率分布直方图1中的a的值;并作出甲种酸奶日销售量的频率分布直方图;
(Ⅱ)记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为s${\;}_{1}^{2}$,s${\;}_{2}^{2}$,试比较s${\;}_{1}^{2}$与s${\;}_{2}^{2}$的大小;(只需写出结论)
(Ⅲ)假设同一组中的每个数据可用该该组区间的中点值代替,试估计乙种酸奶在未来一个月(按30天计箅)的销售量总量.
| 分组(日销售量) | 频率(甲种酸奶) |
| [0,10] | 0.10 |
| (10,20] | 0.20 |
| (20,30] | 0.30 |
| (30,40] | 0.25 |
| (40,50] | 0.15 |

(Ⅰ)写出频率分布直方图1中的a的值;并作出甲种酸奶日销售量的频率分布直方图;
(Ⅱ)记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为s${\;}_{1}^{2}$,s${\;}_{2}^{2}$,试比较s${\;}_{1}^{2}$与s${\;}_{2}^{2}$的大小;(只需写出结论)
(Ⅲ)假设同一组中的每个数据可用该该组区间的中点值代替,试估计乙种酸奶在未来一个月(按30天计箅)的销售量总量.
4.抛物线x2=4y的焦点到准线的距离为( )
0 246642 246650 246656 246660 246666 246668 246672 246678 246680 246686 246692 246696 246698 246702 246708 246710 246716 246720 246722 246726 246728 246732 246734 246736 246737 246738 246740 246741 246742 246744 246746 246750 246752 246756 246758 246762 246768 246770 246776 246780 246782 246786 246792 246798 246800 246806 246810 246812 246818 246822 246828 246836 266669
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |