9．已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点为F，短轴的一个端点为M，直线l：3x-4y=0交椭圆E于A，B两点，若|AF|+|BF|=4，点M到直线l的距离不小于$\frac{4}{5}$，则椭圆E的离心率的取值范围是（ ）
| A． | （0，$\frac{\sqrt{3}}{2}$] | B． | （0，$\frac{3}{4}$] | C． | [$\frac{\sqrt{3}}{2}$，1） | D． | [$\frac{3}{4}$，1） |
8．变量x，y满足约束条件$\left\{\begin{array}{l}{x+y≥0}\\{x-2y+2≥0}\\{mx-y≤0}\end{array}\right.$，若z=2x-y的最大值为2，则实数m等于（ ）
| A． | -2 | B． | -1 | C． | 1 | D． | 2 |
7．某几何体的三视图如图所示，则该几何体的表面积等于（ ）
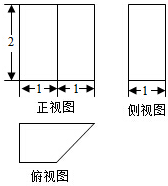
| A． | 8+2$\sqrt{2}$ | B． | 11+2$\sqrt{2}$ | C． | 14+2$\sqrt{2}$ | D． | 15 |
6．
如图，矩形ABCD中，点A在x轴上，点B的坐标为（1，0），且点C与点D在函数f（x）=$\left\{\begin{array}{l}{x+1，}&{x≥0}\\{-\frac{1}{2}x+1，}&{x＜0}\end{array}\right.$的图象上，若在矩形ABCD内随机取一点，则此点取自阴影部分的概率等于（ ）
如图，矩形ABCD中，点A在x轴上，点B的坐标为（1，0），且点C与点D在函数f（x）=$\left\{\begin{array}{l}{x+1，}&{x≥0}\\{-\frac{1}{2}x+1，}&{x＜0}\end{array}\right.$的图象上，若在矩形ABCD内随机取一点，则此点取自阴影部分的概率等于（ ）| A． | $\frac{1}{6}$ | B． | $\frac{1}{4}$ | C． | $\frac{3}{8}$ | D． | $\frac{1}{2}$ |
5．设$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（1，1），$\overrightarrow{c}$=$\overrightarrow{a}$+k$\overrightarrow{b}$，若$\overrightarrow{b}⊥\overrightarrow{c}$，则实数k的值等于（ ）
| A． | -$\frac{3}{2}$ | B． | -$\frac{5}{3}$ | C． | $\frac{5}{3}$ | D． | $\frac{3}{2}$ |
4．若sinα=-$\frac{5}{13}$，则α为第四象限角，则tanα的值等于（ ）
| A． | $\frac{12}{5}$ | B． | -$\frac{12}{5}$ | C． | $\frac{5}{12}$ | D． | -$\frac{5}{12}$ |
2．阅读如图所示的程序框图，运行相应的程序，若输入x的值为1，则输出y的值为（ ）
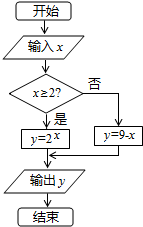
| A． | 2 | B． | 7 | C． | 8 | D． | 128 |
1．下列函数为奇函数的是（ ）
| A． | y=$\sqrt{x}$ | B． | y=ex | C． | y=cosx | D． | y=ex-e-x |
20．若集合M={x|-2≤x＜2}，N={0，1，2}，则M∩N=（ ）
0 246369 246377 246383 246387 246393 246395 246399 246405 246407 246413 246419 246423 246425 246429 246435 246437 246443 246447 246449 246453 246455 246459 246461 246463 246464 246465 246467 246468 246469 246471 246473 246477 246479 246483 246485 246489 246495 246497 246503 246507 246509 246513 246519 246525 246527 246533 246537 246539 246545 246549 246555 246563 266669
| A． | {0} | B． | {1} | C． | {0，1，2} | D． | {0，1} |