13．如图.在直四棱柱ABCD-A1B1C1D1中.四边形ABCD是直角梯形.∠DAB=90°.AA1=AB=BC=2.AD=1．(1)证明:在平面BB1C上.一定存在过点C的直线l与直线A1D平行．——青夏教育精英家教网——

如图，在直四棱柱ABCD-A₁B₁C₁D₁中，四边形ABCD是直角梯形，∠DAB=90°，AA₁=AB=BC=2，AD=1．
（1）证明：在平面BB₁C上，一定存在过点C的直线l与直线A₁D平行．
（2）求二面角A₁-CD-A的余弦值．

12．设x，y满足条件$\left\{\begin{array}{l}{0≤x≤0}\\{0≤y≤2}\\{2x-y≥1}\end{array}\right.$，则t=2y-x的最大值为（　　）

11．在△ABC中，角A、B、C所对的边分别为a，b，c，已知2sinAsinB=2sin²A+2sin²B+cos2C-1
（1）求∠C的大小；
（2）若a-2b=1，且△ABC的面积为$\frac{5\sqrt{3}}{2}$，求边a的长．

10．已知y=f（x）是定义域为R的单调函数，且x₁≠x₂，λ≠-1，α=$\frac{{{x_1}+λ{x_2}}}{1+λ}，β=\frac{{{x_2}+λ{x_1}}}{1+λ}$，若|f（x₁）-f（x₂）|＜|f（α）-f（β）|，则（　　）

9．某工厂生产某种零件，每日生产成本为1000元，此零件每天的批发价和产量均具有随机性，且互不影响．其具体情况如下表：

日产量	400	500		批发价	8	10
概率	0.4	0.6		概率	0.5	0.5

（1）设随机变量X表示生产这种零件的日利润，求X的分布列及期望；
（2）若该厂连续3天按此情况生产和销售，设随机变量Y表示这3天中利润不少于3000的天数，求Y的数学期望和方差，并求至少有2天利润不少于3000的概率．（注：以上计算所得概率值用小数表示）

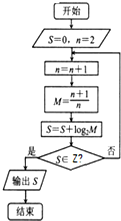
8．执行如图所示的算法，则输出的结果是（　　）

7．有一正四面体，分别标有1，2，3，4，小明和小李分别掷一次，两次向下的面上的数字相加为偶数则小明胜，则小明胜的概率是$\frac{3}{8}$．

6．已知数列{a_n}为等比数列，a₁=1，且a₂，a₃+1，a₄成等差数列．
（Ⅰ）求数列的通项公式a_n；
（Ⅱ）若数列{b_n}满足：b_n=$\frac{a_n}{{（{a_n}+1）（{a_{n+1}}+1）}}$，设其前n项和为S_n，证明：S_n＜$\frac{1}{2}$．

5．边长为$2\sqrt{2}$的正△ABC的三个顶点都在体积是$4\sqrt{3}π$的球面上，则球面上的点到平面ABC的最大距离是$\frac{4\sqrt{3}}{3}$．

如上图，在山顶铁塔上B处测得地面上一点A的俯角为α=60°，在塔底C处
测得A处的俯角为β=45°，已知铁塔BC部分的高为$12\sqrt{3}$米，山高CD=18+6$\sqrt{3}$米．

0 246287 246295 246301 246305 246311 246313 246317 246323 246325 246331 246337 246341 246343 246347 246353 246355 246361 246365 246367 246371 246373 246377 246379 246381 246382 246383 246385 246386 246387 246389 246391 246395 246397 246401 246403 246407 246413 246415 246421 246425 246427 246431 246437 246443 246445 246451 246455 246457 246463 246467 246473 246481 266669