5.已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的两焦点分别是F1,F2,过F1的直线交椭圆于P,Q两点,若|PF2|=|F1F2|,且2|PF1|=3|QF1|,则椭圆的离心率为( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{3\sqrt{2}}{5}$ |
20.过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的一个焦点F1作一条渐近线的垂线,垂足为A,与另一条渐近线交于点B,若A恰好是F1B的中点,则双曲线的离心率是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
18.某工厂对同时生产某件产品的件数x(单位:件)与所用时间y(单位:小时)进行了测验.测验结果如下表所示:
(1)求出y与x的线性回归方程$\widehat{y}$=bx+a;
(2)试预测同时生产20件该产品需要多少小时?
(附:线性回归方程$\widehat{y}$=bx+a中,b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}-b\overline{x}$)
| 件数x(件) | 11 | 12 | 13 |
| 时间y(小时) | 25 | 26 | 30 |
(2)试预测同时生产20件该产品需要多少小时?
(附:线性回归方程$\widehat{y}$=bx+a中,b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}-b\overline{x}$)
17.已知双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0),右焦点为F,过F作一条渐近线的垂线,垂足为M,O为坐标原点,若△OMF面积为$\frac{\sqrt{3}}{8}{c}^{2}$(其中c为半焦距),则该双曲线离心率可能为( )
0 245570 245578 245584 245588 245594 245596 245600 245606 245608 245614 245620 245624 245626 245630 245636 245638 245644 245648 245650 245654 245656 245660 245662 245664 245665 245666 245668 245669 245670 245672 245674 245678 245680 245684 245686 245690 245696 245698 245704 245708 245710 245714 245720 245726 245728 245734 245738 245740 245746 245750 245756 245764 266669
| A. | $\sqrt{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | 3 | D. | 2$\sqrt{3}$ |
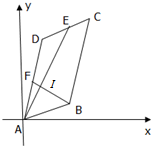 如图,已知平行四边形ABCD的顶点A(0,0),B(4,1),C(6,8)
如图,已知平行四边形ABCD的顶点A(0,0),B(4,1),C(6,8) 如图,△ABC是圆O的内接三角形,PA是圆O的切线,A为切点,PB交AC于点E,交圆O于点D,若PE=PA,∠ABC=60°,且PD=2,BD=6,则AC=6.
如图,△ABC是圆O的内接三角形,PA是圆O的切线,A为切点,PB交AC于点E,交圆O于点D,若PE=PA,∠ABC=60°,且PD=2,BD=6,则AC=6.